第一章:前言
1.1 概述
- 计算机的底层只有
二进制,即计算机中运算和存储的所有数据都需要转换为二进制,包括:数字、字符、图片、视频等。

1.2 冯·诺依曼体系结构
- 之前,我们也提到现代的计算机(量子计算机除外)几乎都遵循
冯·诺依曼体系结构,其理论要点如下:- ① 存储程序:
程序指令和数据都存储在计算机的内存中,这使得程序可以在运行时修改。 - ② 二进制逻辑:所有数据和指令都以
二进制形式表示。 - ③ 顺序执行:指令按照它们在内存中的顺序执行,但可以有条件地改变执行顺序。
- ④ 五大部件:计算机由
运算器、控制器、存储器、输入设备和输出设备组成。 - ⑤ 指令结构:指令由操作码和地址码组成,操作码指示要执行的操作,地址码指示操作数的位置。
- ⑥ 中心化控制:计算机的控制单元(CPU)负责解释和执行指令,控制数据流。
- ① 存储程序:
提醒
冯·诺依曼体系结构决定了计算机为什么只能识别二进制!!!
第二章:进制
2.1 常见的进制
- 在生活中,我们最为常用的进制就是
十进制,其规则是满 10 进 1,即:

- 在计算机中,常见的进制有
二进制、八进制和十六进制,即:- 二进制:只能 0 和 1 ,满 2 进 1 。
- 八进制:0 ~ 7 ,满 8 进 1 。
- 十六进制:0 ~ 9 以及 A ~ F ,满 16 进 1 。
提醒
- ① 在十六进制中,除了
0到9这十个数字之外,还引入了字母,以便表示超过9的值。 - ② 其中,字母
A对应十进制的10,字母B对应十进制的11,字母C对应十进制的12,字母D对应十进制的13,字母E对应十进制的14,字母F对应十进制的15。
- 进制的换算举例,如下所示:
| 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | a 或 A |
| 11 | 1011 | 13 | b 或 B |
| 12 | 1100 | 14 | c 或 C |
| 13 | 1101 | 15 | d 或 D |
| 14 | 1110 | 16 | e 或 E |
| 15 | 1111 | 17 | f 或 F |
| 16 | 10000 | 20 | 10 |
| ... | ... | ... | ... |
- 二进制和十六进制的关系:十六进制是以 16 为基数的进制系统,16 在二进制中表示为 ( 2^4 ),即:一个十六进制可以表示 4 位二进制。
提醒
十六进制的范围是:0 ~ F (0 ~ 15)对应的二进制数的范围是:0000 ~ 1111 (0 ~ 15)。
- 每个十六进制数都可以映射到一个唯一的 4 位二进制数,即:
| 十六进制 | 二进制 |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
提醒
由此可见,每个十六进制数字确实由 4 位二进制数表示。
- 二进制和八进制的关系:八进制是以 8 为基数的进制系统,8 在二进制中表示为 ( 2^3 );即:一个八进制位可以表示 3 个二进制位。
提醒
八进制的范围是:0 ~ 7 对应的二进制数的范围是:000 ~ 111。
- 每个八进制数位都可以映射到一个唯一的 3 位二进制数,即:
| 八进制 | 二进制 |
|---|---|
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
提醒
由此可见,每个八进制数字确实由 3 位二进制数表示。
2.2 C 语言中如何表示不同进制的整数?
规则如下:
- 在 C 语言中,如果是
二进制(字面常量),则需要在二进制整数前加上0b或0B。 - 在 C 语言中,如果是
八进制(字面常量),则需要在八进制整数前加上0。 - 在 C 语言中,如果是
十进制(字面常量),正常数字表示即可。 - 在 C 语言中,如果是
十六进制(字面常量),则需要在十六进制整数前加上0x或0X。
- 在 C 语言中,如果是
示例:
#include <stdio.h>
int main() {
// 禁用 stdout 缓冲区
setbuf(stdout, nullptr);
int num1 = 0b10100110; // 二进制
int num2 = 0717563; // 八进制
int num3 = 1000; // 十进制
int num4 = 0xaf72; // 十六进制
printf("num1 = %d\n", num1); // num1 = 166
printf("num2 = %d\n", num2); // num2 = 237427
printf("num3 = %d\n", num3); // num3 = 1000
printf("num4 = %d\n", num4); // num4 = 44914
return 0;
}2.3 输出格式
- 在 C 语言中,可以使用不同的
格式占位符来输出不同进制的整数,如下所示:%b:二进制整数^c23。%d:十进制整数。%o:八进制整数。%x:十六进制整数。%#o:显示前缀0的八进制整数。%#x:显示前缀0x的十六进制整数。%#X:显示前缀0X的十六进制整数。
注意
- ① 在 C23 标准之前,C 语言中的
scanf函数和printf函数,都不支持二进制整数,也没有对应的格式占位符。 - ② 在 C23 标准之后,C 语言中的
scanf函数和printf函数,都支持二进制整数,其对应的格式占位符是%b。
- 示例:
#include <stdio.h>
int main() {
// 禁用 stdout 缓冲区
setbuf(stdout, nullptr);
int num = 100;
// 100 的二进制整数: 1100100
printf("%d 的二进制整数: %b\n", num, num);
// 100 的十进制整数: 100
printf("%d 的十进制整数: %d\n", num, num);
// 100 的八进制整数: 144
printf("%d 的八进制整数: %o\n", num, num);
// 100 的十六进制整数: 64
printf("%d 的十六进制整数: %x\n", num, num);
// 100 的八进制(前缀)整数: 0144
printf("%d 的八进制(前缀)整数: %#o\n", num, num);
// 100 的十六进制(前缀)整数: 0x64
printf("%d 的十六进制(前缀)整数: %#x\n", num, num);
// 100 的十六进制(前缀)整数: 0X64
printf("%d 的十六进制(前缀)整数: %#X\n", num, num);
return 0;
}第三章:进制的运算规则
3.1 概述
十进制的运算规则:- 逢
十进一(针对加法而言)。 - 借
一当十(针对减法而言)。
- 逢
二进制的运算规则:- 逢
二进一(针对加法而言)。 - 借
一当二(针对减法而言)。
- 逢
八进制的运算规则:- 逢
八进一(针对加法而言)。 - 借
一当八(针对减法而言)。
- 逢
十六进制的运算规则:- 逢
十六进一(针对加法而言)。 - 借
一当十六(针对减法而言)。
- 逢
3.2 二进制的运算
3.2.1 二进制加法
- 二进制加法举例,如下所示:
1 + 0 = 1
1 + 1 = 10
11 + 10 = 101
111 + 111 = 1110- 其对应的图示,如下所示:
3.2.2 二进制减法
- 二进制减法举例,如下所示:
1 - 0 = 1
10 - 1 = 1
101 - 11 = 10
1100 - 111 = 101- 其对应的图示,如下所示:
3.3 八进制的运算
3.3.1 八进制加法
- 八进制加法举例,如下所示:
3 + 4 = 7
5 + 6 = 13
75 + 42 = 137
2427 + 567 = 3216- 其对应的图示,如下所示:
3.3.2 八进制减法
- 八进制减法举例,如下所示:
6 - 4 = 2
52 - 27 = 33
307 - 141 = 146
7430 - 1451 = 5757- 其对应的图示,如下所示:
3.4 十六进制的运算
3.4.1 十六进制加法
- 十六进制加法举例,如下所示:
6 + 7 = D
18 + BA = D2
595 + 792 = D27
2F87 + F8A = 3F11- 其对应的图示,如下所示:
3.4.2 十六进制减法
- 十六进制减法举例,如下所示:
D - 3 = A
52 - 2F = 23
E07 - 141 = CC6
7CA0 - 1CB1 = 5FEF- 其对应的图示,如下所示:
第四章:进制的转换
4.1 概述
- 不同进制的转换,如下所示:
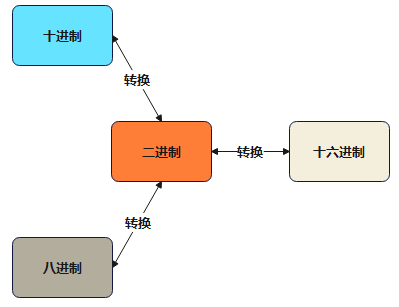
- 在计算机中,数据是从右往左的方式排列的;其中,最右边的是低位,最左边的是高位,即:
4.2 二进制和十进制的转换
4.2.1 二进制转换为十进制
- 规则:从最低位开始,将每个位上的数提取出来,乘以 2 的 (位数 - 1 )次方,然后求和。
提醒
- ① 在学术界,将这种计算规则,称为
位权相加法。 - ②
八进制转换为十进制、十六进制转换为十进制和二进制转换为十进制的算法相同!!!
- 示例:十进制转十进制
- 示例:二进制转十进制
4.2.2 十进制转换二进制
- 规则:将该数不断除以 2 ,直到商为 0 为止,然后将每步得到的余数倒过来,就是对应的二进制。
提醒
- ① 在学术界,将这种计算规则,称为
短除法或连续除2取余法。 - ② 很好理解,只有不断地除以 2 ,就能保证最大的数字不超过 2 ,这不就是二进制(只能有 0 或 1)吗?
- ③
八进制转换为二进制、十六进制转换为二进制和十进制转换为二进制的算法相同!!!
- 示例:十进制转十进制
- 示例:十进制转二进制
4.2.3 二进制转八进制
规则:从右向左,每 3 位二进制就是一个八进制,不足补 0(分组转换法)。
示例:011 101 001 -> 351
4.2.4 二进制转十六进制
规则:从右向左,每 4 位二进制就是一个十六进制,不足补 0(分组转换法)。
示例:1110 1001 -> 0xE9
第五章:原码、反码和补码
5.1 概述
- 在计算机中,
无符号位的整数,如:unsinged int 等,在计算机底层存储的是二进制编码。
提醒
所谓无符号位的整数,就是对应数学中的自然数(0 和正整数),即:[0,+∞]。
- 在计算机中,
有符号位的整数,如:int 等,在计算机底层存储的是补码。
提醒
所谓有符号位的整数,就是对应数学中的整数(正整数、0 和负整数),即:[-∞,+∞]。
5.2 机器数和真值
- 机器数:一个数在计算机的存储形式是二进制,我们称这些二进制数为机器数。机器数可以是有符号的,用机器数的最高位来存放符号位,
0表示正数,1表示负数。
重要
- ① 这里讨论的适用于
有符号位的整数,如:int 等。 - ② 这里讨论的不适用于
无符号位的整数,即:unsinged int 等。
- 真值(数据位):因为机器数带有符号位,所以机器数的形式值不等于其真实表示的值(真值),以机器数 1000 0001 为例,其真正表示的值(首位是符号位)为 -1,而形式值却是 129 ,因此将带有符号位的机器数的真正表示的值称为机器数的真值。
重要
- ① 这里讨论的适用于
有符号位的整数,如:int 等。 - ② 这里讨论的不适用于
无符号位的整数,即:unsinged int 等。
5.3 原码
- 原码的表示与机器数真值表示的一样,即用第一位表示符号,其余位表示数值。
- 原码的规则:
提醒
- 正数的
原码是它本身对应的二进制数,符号位是 0 。 - 负数的
原码是它本身绝对值对应的二进制数,但是符号位是 1 。
+1的原码,使用16位二进数来表示,就是:
| 十进制数 | 原码(16位二进制数) |
|---|---|
| +1 | 0000 0000 0000 0001 |
-1的原码,使用16位二进数来表示,就是:
| 十进制数 | 原码(16位二进制数) |
|---|---|
| -1 | 1000 0000 0000 0001 |
重要
- ① 按照原码的规则,会出现
+0和-0的情况,即:0000 0000 0000 0001(+0)、1000 0000 0000 0001(-0),显然不符合实际情况。 - ② 所以,计算机底层虽然存储和计算的都是二进数,但显然不是原码。
5.4 反码
- 反码的规则:
提醒
- 正数的
反码和它的原码相同。 - 负数的
反码是在其原码的基础上,符号位不变,其余各位取反。
+1的反码,使用16位二进数来表示,就是:
| 十进制数 | 原码(16位二进制数) | 反码(16位二进制数) |
|---|---|---|
| +1 | 0000 0000 0000 0001 | 0000 0000 0000 0001 |
-1的反码,使用16位二进数来表示,就是:
| 十进制数 | 原码(16位二进制数) | 反码(16位二进制数) |
|---|---|---|
| -1 | 1000 0000 0000 0001 | 1111 1111 1111 1110 |
重要
- ① 按照反码的规则,如果是
+0,对应的原码是0000 0000 0000 0000;那么,其反码还是0000 0000 0000 0000;如果是-0,对应的原码是1000 0000 0000 0000,其反码是1111 1111 1111 1111,显然不符合实际情况。 - ② 所以,计算机底层虽然存储和计算的都是二进数,但显然不是反码。
5.5 补码
- 补码的规则:
提醒
- 正数的
补码和它的原码相同。 - 负数的
补码是在其反码的基础上 + 1 。
+1的补码,使用16位二进数来表示,就是:
| 十进制数 | 原码(16位二进制数) | 反码(16位二进制数) | 补码(16位二进制数) |
|---|---|---|---|
| +1 | 0000 0000 0000 0001 | 0000 0000 0000 0001 | 0000 0000 0000 0001 |
-1的补码,使用16位二进数来表示,就是:
| 十进制数 | 原码(16位二进制数) | 反码(16位二进制数) | 补码(16位二进制数) |
|---|---|---|---|
| -1 | 1000 0000 0000 0001 | 1111 1111 1111 1110 | 1111 1111 1111 1111 |
- 如果
0,按照+0的情况进行处理,如下所示:
0 ,按照 +0 的情况进行处理- 如果
0,按照-0的情况进行处理,如下所示:
0 ,按照 -0 的情况进行处理+1和-1的原码和补码的转换过程,如下所示:
+1 和 -1 的原码和补码的转换过程重要
- ① 补码表示法解决了
原码和反码存在的两种零(+0和-0)的问题,即:在补码表示法中,只有一个零,即0000 0000。 - ②补码使得
加法运算和减法运算可以统一处理,通过将减法运算转换为加法运算,可以简化硬件设计,提高了运算效率。 - ③ 计算机底层
存储和计算的都是二进数的补码。换言之,当读取整数的时候,需要采用逆向的转换,即:将补码转换为原码。正数的原码、反码、补码都是一样的,三码合一。负数的补码转换为原码的方法就是先减去1,得到反码,再按位取反,得到原码(符号位是不能借位的)。
5.6 总结
- ① 计算机底层
存储和计算的都是二进数的补码。换言之,当读取整数的时候,需要采用逆向的转换,即:将补码转换为原码。 - ② 正数的原码、反码和补码都是一样的,三码合一。
- ③ 负数的反码是在其原码的基础上,按位取反(0 变 1 ,1 变 0 ),符号位不变;负数的补码是其反码 + 1 。
- ④ 0 的补码是 0 。
- ⑤ 负数的补码转换为原码的方法就是先减去
1,得到反码,再按位取反,得到原码(符号位是不能借位的)。
第六章:计算机底层为什么使用补码?
6.1 概述
加法和减法是计算机中最基本的运算,计算机时时刻刻都离不开它们,所以它们由硬件直接支持。为了提高加法和减法的运行效率,硬件电路必须设计得尽量简单。对于有符号位的数字来说,内存需要区分符号位和数值位:对于人类来说,很容易识别(最高位是 0 还是 1);但是,对于计算机来说,需要设计专门的电路,这无疑增加了硬件的复杂性,增加了计算时间。如果能将符号位和数值位等同起来,让它们一起参与运算,不再加以区分,这样硬件电路就可以变得非常简单。
此外,加法和减法也可以合并为一种运算,即:加法运算。换言之,减去一个数就相当于加上这个数的相反数,如:
5 - 3相当于5 +(-3),10 -(-9)相当于10 + 9。如果能够实现上述的两个目标,那么只需要设计一种简单的、不用区分符号位和数值位的加法电路,就能同时实现加法运算和减法运算,而且非常高效。其实,这两个目标已经实现了,真正的计算机的硬件电路就是这样设计的。
但是,简化硬件电路是有代价的,这个代价就是
有符号数在存储和读取的时候都要继续转换。这也是对于有符号数的运算来说,计算机底层为什么使用补码的原因所在。
6.2 补码到底是如何简化硬件电路的?
- 假设 6 和 18 都是 short 类型,现在我们要计算
6 - 18的结果,根据运算规则,它等价于6 +(-18)。如果按照采用原码来计算,那么运算过程是这样的,如下所示:
提醒
直接使用原码表示整数,让符号位也参与运算,那么对于减法来说,结果显然是不正确的。
- 于是,人们开始继续探索,不断试错,终于设计出了
反码,如下所示:
提醒
直接使用反码表示整数,让符号位也参与运算,对于 6 +(-18)来说,结果貌似正确。
- 如果我们将
被减数和减数对调一下,即:计算18 - 6的结果,也就是18 +(-6)的结果,继续采用反码来进行运算,如下所示:
提醒
- ① 6 - 18,即:6+(-18),如果采用
反码计算,结果是正确的;但是,18 - 6,即:18 +(-6),如果采用反码计算,结果相差 1 。 - ② 可以推断:如果按照
反码来计算,小数 - 大数,结果正确;而大数 - 小数,结果相差 1 。
- 对于这个相差的
1必须进行纠正,但是又不能影响小数-大数的结果。于是,人们又绞尽脑汁设计出了补码,给反码打了一个“补丁”,终于把相差的1给纠正过来了。那么,6 - 18按照补码的运算过程,如下所示:
- 那么,
18 - 6按照补码的运算过程,如下所示:
重要
总结:采用补码的形式正好将相差的 1纠正过来,也没有影响到小数减大数,这个“补丁”非常巧妙。
- ① 小数减去大数,结果为负,之前(负数从反码转换为补码需要 +1)加上的 1 ,后来(负数从补码转换为反码要 -1)还需要减去,正好抵消掉,所以不会受到影响。
- ② 大数减去小数,结果为正,之前(负数从反码转换为补码需要 +1)加上的 1 ,后来(正数的补码和反码相同,从补码转换为反码不用 -1)就没有再减去,不能抵消掉,这就相当于给计算结果多加了一个 1。
补码这种天才般的设计,一举达成了之前加法运算和减法运算提到的两个目标,简化了硬件电路。
6.3 问题抛出
- 在 C 语言中,对于
有符号位的整数,是使用0作为正数,1作为负数,来表示符号位,并使用数据位来表示的是数据的真值,如下所示:
int a = 10;
int b = -10;- 但是,对于
无符号位的整数而言,是没有符号位和数据位,即:没有原码、反码、补码的概念。无符号位的整数的数值都是直接使用二进制来表示的(也可以理解为,对于无符号位的整数,计算机底层存储的就是其原码),如下所示:
unsigned int a = 10;
// 其实是不对的,因为无符号位只能是自然数;但是,C 语言就是这么坑爹!!!
unsigned int b = -10;- 这就是导致了一个结果就是:如果我定义一个
有符号的负数,却让其输出无符号,必然造成结果不对,如下所示:
#include <stdio.h>
char *getBinary(int num) {
static char binaryString[33];
int i, j;
for (i = sizeof(num) * 8 - 1, j = 0; i >= 0; i--, j++) {
const int bit = (num >> i) & 1;
binaryString[j] = bit + '0';
}
binaryString[j] = '\0';
return binaryString;
}
int main() {
// 禁用 stdout 缓冲区
setbuf(stdout, NULL);
int num = -10;
printf("b=%s\n", getBinary(num)); // b=11111111111111111111111111110110
printf("b=%d\n", num); // b=-10
printf("b=%u\n", num); // b=4294967286
return 0;
}- 其实,C 语言的底层逻辑很简单,C 语言压根不关心你定义的是
有符号数还是无符号数,它只关心内存(如果定义的是有符号数,那就按照有符号数的规则来存储;如果定义的是无符号数,那就按照无符号数的规则来存储)。换言之,有符号数可以按照无符号数的规则来输出,无符号数也可以按照有符号数的规则来输出,至于输出结果对不对,那是程序员的事情,和 C 语言没有任何关系。
重要
- ① 实际开发中,
printf函数中的常量、变量或表达式,需要和格式占位符一一对应;否则,将会出现数据错误的现象。 - ② 正因为上述的原因,很多现代化的编程语言,如:Java 等,直接取消了无符号的概念。但是,很多数据库是使用 C 语言开发的,如:MySQL 等,就提供了创建数据表的字段为无符号类型的功能,即:
UNSIGNED(正整数) ,不要感觉困惑!!! - ③ 对于
1000 0000 …… 0000 0000这个特殊的补码,无法按照上述的方法转换为原码,所以计算机直接规定这个补码对应的值就是-2³¹,至于为什么,下节我们会详细分析。
第七章:位权相加法
7.1 概述
- 在上文,在提起
二进制转换为十进制的时候,我们就提到了位权相加法,例如:1011 --> 11。
7.2 无符号位整数的位权相加法
在计算机中,
无符号位的整数,如:unsinged int 等,在计算机底层存储的是二进制编码。对于一个
无符号整数,在计算机底层存储的二进制是;那么,其对应的 十进制是。 示例:1010 1010 -> 170
1010 1010 = 1×2⁷ + 1×2⁵ + 1×2³ + 1×2¹ = 1707.3 有符号位整数的位权相加法
在计算机中,
有符号位的整数,如:int 等,在计算机底层存储的是补码。对于一个
有符号整数,在计算机底层存储的二进制是;那么,其对应的 十进制是。 示例:0010 1010 --> 42
0010 1010 = 1×2⁵ + 1×2³ + 1×2¹ = 42- 示例:1010 1010 --> -86
1010 1010 = -1×2⁷ + 1×2⁵ + 1×2³ + 1×2¹ = -867.4 有符号位整数的三个特性
- ① 对于一个
8位的有符号位整数,其最大的负数-1,在计算机底层的补码是1111 1111。
1111 1111
= -1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁴ + 1×2³ + 1×2² + 1×2¹ + 1×2⁰
= -1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁴ + 1×2³ + 1×2² + 1×2¹ + 1×2⁰ + 1×2⁰ - 1×2⁰
= -1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁴ + 1×2³ + 1×2² + 1×2¹ + 1×2¹ - 1×2⁰
= -1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁴ + 1×2³ + 1×2² + 1×2² - 1×2⁰
= -1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁴ + 1×2³ + 1×2³ - 1×2⁰
= -1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁴ + 1×2⁴ - 1×2⁰
= -1×2⁷ + 1×2⁶ + 1×2⁵ + 1×2⁵ - 1×2⁰
= -1×2⁷ + 1×2⁶ + 1×2⁶ - 1×2⁰
= -1×2⁷ + 1×2⁷ - 1×2⁰
= -1- ② x + (-x) = 10000 ... 0000 。其中,x 是自然数,如:1、2 等;10000 ... 0000 中有 n 个 0 ,1 会溢出,会被丢弃。
问:如果一个有符号数,在计算机中的存储是 1101 0100(补码) ,求其相反数的二进制表示?
答:从右往左数,第一个为 1 的数,保留下来(100),其余按位取反,即:0010 1100- ③ x + (~x) = 1111 ... 1111 = -1 。其中,1111 ... 1111 有 n 个 1 ,就是 -1 。
第八章:从设计者的角度看原码、反码和补码
8.1 概述
原码、反码和补码的计算方式,我们已经有所了解了。
提醒
- 原码:十进制数据的二进制表现形式,最左边的是符号位,0 为正,1 为负。
- 反码:正数的反码是其本身,负数的反码是符号位保持不变,其余位取反。
- 补码:正数的补码是其本身,负数的补码是在其反码的基础上 + 1 。
- 但是,如果你还是感觉很模糊,不妨看看下面的内容,或许会让你有所感悟!!!
8.2 原码
8.2.1 概述
原码就是十进制数据的二进制表现形式,最左边的是符号位,0 为正,1 为负。
假设一个整数是
56,那么其原码就是0011 1000,如下所示:
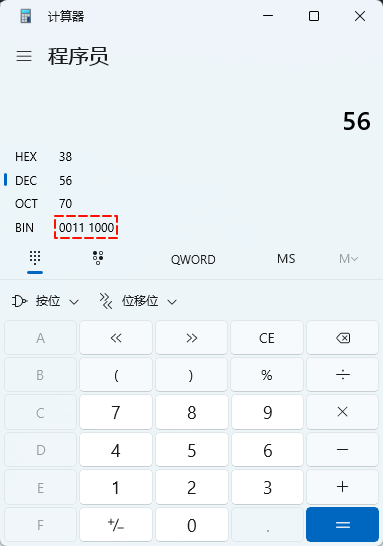
字节(Byte)是计算机中数据存储和传输的基本单位(最小计量单位),它通常由 8 个位(bit)组成。
8.2.2 最大值
- 按照原码的表示形式,1 个字节的最大值,在计算机底层就应该是
0111 1111,如下所示:
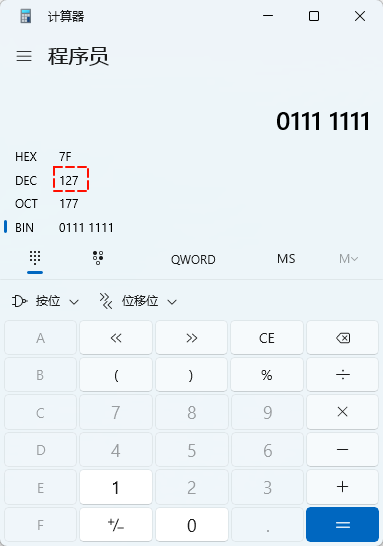
- 按照原码的表示形式,1 个字节的最大值,转换为十进制就应该是:
127,如下所示:
提醒
手动计算的技巧:0111 1111 = 1000 0000 - 1 = 2⁷ - 1 = 128 -1 = +127 。
8.2.3 最小值
- 按照原码的表示形式,1 个字节的最小值,在计算机底层就应该是
1111 1111,如下所示:
提醒
- ① 如果1 个字节的最小值,在计算机底层是
1000 0000,那么转换为十进制整数,就是- 0,而在数学中,没有- 0的概念,或者可以认为- 0就是0。 - ② 所以,按照原码的表示形式,1 个字节的最小值,在计算机底层就应该是
1111 1111。
- 按照原码的表示形式,1 个字节的最小值,转换为十进制就应该是:
-127。
提醒
① 手动计算的技巧:1111 1111 ,抛开符号位去计算,即:0111 1111 = 1000 0000 - 1 = 2⁷ - 1 = 128 -1 = +127 。
② 因为 1111 1111 中的符号位是 1 ,所以最终结果是 -127 。
8.2.4 原码的数值计算
- 在原码中,如果是
正数的话,计算不会有问题,如下所示:
提醒
- ① 0000 0000 + 1 = 0000 0001 = 1 ,计算机底层计算结果和数学结果一致。
- ② 0000 0001 + 1 = 0000 0010 = 2,计算机底层计算结果和数学结果一致。
- ③ ...
- ④ 0111 1110 + 1 = 0111 1111 = 127,计算机底层计算结果和数学结果一致。
- 在原码中,如果是
负数的话,计算会有问题,如下所示:
提醒
- ① 1000 0000 + 1 = 1000 0001 = -1(计算机底层结果值),而 -0 + 1 = 1 (数学结果)。
- ② 1000 0001 + 1 = 1000 0010 = -2(计算机底层结果值),而 -1 + 1 = 0 (数学结果)。
- ③ ...
- ④ 1111 1110 + 1 = 1111 1111 = -127(计算机底层结果值),而 -126 + 1 = -125 (数学结果)。
8.2.5 原码的弊端
- 我们可以结合
数轴来理解,以1000 0000 + 1为例,如下所示:
- 我们可以结合
数轴来理解,以1000 0001 + 1为例,如下所示:
8.2.6 结论
- 如果利用
原码对正数进行计算,结果是不会有问题的。 - 如果利用
原码对负数进行计算,结果就会出错,即:实际运算的结果,和我们预期的结果是相反的。
提醒
方向不对,努力白费,对于负数,只要在计算的时候,将方向改变不就可以了吗?
8.3 反码
8.3.1 概述
为了解决
原码不能计算负数的问题,反码出现了。反码的规则,如下所示:
- ①
正数的反码和它的原码相同。 - ②
负数的反码是在其原码的基础上,符号位不变,其余各位取反。
- ①
假设一个整数是
-56,那么其原码就是1011 1000,如下所示:
- 其反码就是
1100 0111,如下所示:
8.3.2 反码的数值计算
- 如果一个整数是
-56,其原码就是1011 1000,其反码就是1100 0111,如下所示:
- 如果
-56 + 1,其结果应该是-55,其反码,如下所示:
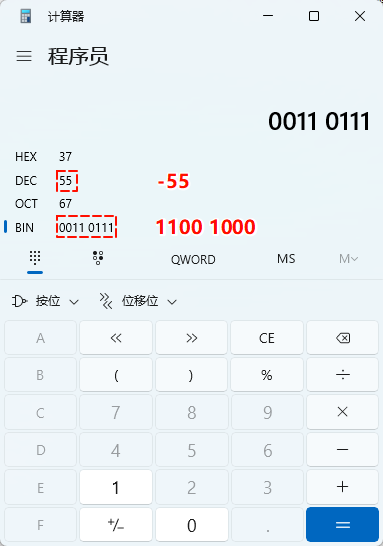
- 我们也可以用
计算器来验证-55的反码,如下所示:
8.3.3 反码的数值计算
- 从上面的答案来说,好像
反码计算负数是没什么问题的;我们可以再次验证一下其它的负数。 -1 ~ -7的原码和反码表,如下所示:
- 以
-4为例,如果按照原码来计算,-4 - 1 = 1000 0100 - 1 = 1000 0011 = -3,结果是不对的,如下所示:
- 以
-4为例,如果按照原码来计算,-4 + 1 = 1000 0100 + 1 = 1000 0101 = -5,结果是不对的,如下所示:
- 以
-4为例,如果按照反码来计算,-4 - 1 = 1111 1011 - 1 = 1111 1010 = -5,结果是正确的,如下所示:
- 以
-4为例,如果按照反码来计算,-4 + 1 = 1111 1011 + 1 = 1111 1100 = -3,结果是正确的,如下所示:
8.3.4 反码的弊端
- 以
-1为例,如果按照反码来计算,-1 - 1 = 1111 1110 - 1 = 1111 1101 = -2,结果是正确的,如下所示:
- 以
-1为例,如果按照反码来计算,-1 + 1 = 1111 1110 + 1 = 1111 1111 = -0,结果好像正确?如下所示:
- 以
-1为例,如果按照反码来计算,-1 + 2 = 1111 1110 + 10 = 0000 0000 = 0,结果是不对的,如下所示:
8.3.5 结论
- 负数运算的时候,如果结果
不跨 0,则没有任何问题;但是如果结果跨 0,和实际结果会有 1 的偏差,因为在反码中有 +0 和 -0 的情况(原码中也有)。
8.4 补码
8.4.1 概述
为了解决
反码计算负数,结果跨 0,实际结果不对的情况,补码出现了。其规则,如下所示:
- ① 正数的
补码和它的原码相同。 - ② 负数的
补码是在其反码的基础上 + 1 。
- ① 正数的
原码、反码和补码表,如下所示:
提醒
正是这种 +1 的技巧,一举消除了 +0 和 -0 的情况,并也间接的解决了反码在计算负数时,结果超过 0 的范围,计算结果和实际结果差 1 的情况。
8.4.2 补码的数值计算
- 以
-4为例,如果按照补码来计算,-4 + 3 = 1111 1100 + 0000 0011 = 1111 1111 = -1,结果是正确,如下所示:
- 我们可以使用
计算器来验证,如下所示:
- 以
-4为例,如果按照补码来计算,-4 + 4 = 1111 1100 + 0000 0100 = 0000 0000 = 0,结果是正确,如下所示:
- 我们可以使用
计算器来验证,如下所示:
8.4.3 特殊情况
- 因为
补码是在反码的基础上+ 1得到的,所以-127的补码是1000 0001,如下所示:
- 因为一个字节是 8 bit,而 8 bit 可能表示 2^8 = 256 个数字,正数是 0 ~ 127 共 128 个,而负数到目前为止只有 127 个,此时一共 255 个数字;所以,计算机规定 1000 0000 就是 -128 的补码,这样就可以表示 256 个数字了,如下所示:
8.4.4 结论
- 对于
整数而言,在计算机中存储和计算都是以补码的形式进行的。