第一章：前言

1.1 运算符、表达式和操作数

运算符就是对常量或变量进行操作的符号，如下所示：

表达式是由变量、常量（也称为操作数）和运算符（也称为操作符）组成的序列，表达式一定具有值，如下所示：

提醒

① 表达式可以非常简单，如：一个单独的常量或变量。
② 表达式可以非常复杂，如：包含多个运算符或函数调用的结合。
③ 表达式的作用就是计算值，如：赋值、函数调用等。
④ 判断表达式的最简单方法：拿一个变量去接收表达式（值），看是否成立（因为表达式的作用就是计算值）？
- 如：int num = 10; 中的 10 就是表达式。
- 如：int num = a + b; 中的 a+b 就是表达式。
- 如：int num = sum(1,2); 中的 sum(1,2) 就是表达式。
- 如：int num = sum(a,b); 中的 sum(a,b) 就是表达式。
- ...

操作数指的是参与运算的值或者对象，如下所示：

语句是代码中一个完整的、可以执行的步骤。

提醒

① 语句要么以 ; 分号简单结尾，即：简单语句；要么以 {} 代码块结尾，即：复合语句。
② 语句的作用复杂多样，常用于构建程序逻辑，如：循环语句、条件判断语句、跳转语句。
③ 很多人也会将语句称为结构，如：循环结构、分支结构。

在 C 语言中，语句和表达式没有明显的绝对界限，它们之间的关系是：
- ① 表达式可以构成语句：许多语句都是由表达式构成的，例如：赋值语句 a = 5; 中，a = 5 是表达式，整个 a = 5; 则是语句。
- ② 语句可以包含表达式：流程控制语句，如： if、while 等，通常在判断条件中包含表达式，条件表达式会返回一个值（真或假），决定是否执行某段代码。

提醒

① 区分语句和表达式最明显的领域，应该属于前端 JavaScript 框架中的 React。
② 在 React 中，其明确要求JSX必须是表达式，而不能是语句。

点我查看

jsx

import React from 'react'

function Greeting(props) {
    let element;
    // 这是一个语句块，使用 if 语句来决定渲染的内容
    if (props.isLoggedIn) {
      element = <h1>Welcome back!</h1>;
    } else {
      element = <h1>Please sign up.</h1>;
    }
    // JSX 是表达式，最终返回由语句决定的 JSX 结构
    return (
      <div> 
          { element } // [!code highlight]  
      </div>
    );
}

export default Greeting;

1.2 运算符的分类

在表达式中，最重要、最核心的就是连接表达式中常量和变量的运算符。
在 C 语言中，根据操作数的个数，可以将运算符分为：

运算符类别	描述	范例
一元运算符（一目运算符）	只需要 `1` 个操作数的运算符。	`+1`
二元运算符（二目运算符）	只需要 `2` 个操作数的运算符。	`a + b`
三元运算符（三目运算符）	只需要 `3` 个操作数的运算符。	`a > b ? a : b`

在 C 语言中，根据功能，可以将运算符分为：

运算符类别	描述	常见的运算符
算术运算符	用于进行基本的数学运算的运算符。	`+`、`-`、`*`、`/`、`%`、`++`、`--`
关系运算符（比较运算符）	用于比较两个值之间的大小或相等性的运算符。	`==`、`!=`、`<`、`>`、`<=`、`>=`
逻辑运算符	用于执行布尔逻辑操作的运算符，通常用于分支结构和循环结构。	`&&`、`\|\|`、`!`
赋值运算符	用于给变量赋值，或通过某种操作更新变量的值的运算符。	`=`、`+=`、`-=`、`*=`、`/=`、`%=`、`<<=`、`>>=`、`&=`、`^=`、`\|=`
位运算	用于对整数的二进制位进行操作的运算符。	`&`、`\|`、`^`、`~`、`<<`、`>>`
三元运算符	简化条件判断的运算符，用于根据条件选择两个值中的一个。	`?:`

提醒

掌握一个运算符，需要关注以下几个方面：

① 运算符的含义。
② 运算符操作数的个数。
③ 运算符所组成的表达式。
④ 运算符有无副作用，即：运算后是否会修改操作数的值。

1.3 优先级和结合性（⭐）

1.3.1 概述

在数学中，如果一个表达式是 a + b * c ，我们知道其运算规则就是：先算乘除再算加减。
C 语言中也是一样，先算乘法再算加减，即：C 语言中乘除的运算符比加减的运算符要高。

1.3.2 优先级和结合性

优先级和结合性的定义，如下所示：
- ① 所谓的优先级：就是当多个运算符出现在同一个表达式中时，先执行哪个运算符。
- ② 所谓的结合性：就是当多个相同优先级的运算符出现在同一个表达式中的时候，是从左到右运算，还是从右到左运算。
  - 左结合性：具有相同优先级的运算符将从左到右（➡️）进行计算。
  - 右结合性：具有相同优先级的运算符将从右到左（⬅️）进行计算。

提醒

优先级和结合性，到底怎么看？

① 先看优先级。
② 如果优先级相同，再看结合性。

C 语言中运算符和结合性的列表，如下所示：

优先级	运算符	名称或含义	结合方向
`0`	`()`	小括号，最高优先级	➡️（从左到右）
`1`	`++`、`--`	后缀自增和自减，如：`i++`、`i--` 等	➡️（从左到右）
	`()`	小括号，函数调用，如：`sum(1,2)` 等
	`[]`	数组下标，如：`arr[0]`、`arr[1]` 等
	`.`	结构体或共用体成员访问
	`->`	结构体或共用体成员通过指针访问
`2`	`++`、`--`	前缀自增和自减，如：`++i`、`--i` 等	⬅️（从右到左）
	`+`	一元加运算符，表示操作数的正，如：`+2` 等
	`-`	一元减运算符，表示操作数的负，如：`-3` 等
	`!`	逻辑非运算符（逻辑运算符）
	`~`	按位取反运算符（位运算符）
	`(typename)`	强制类型转换
	`*`	解引用运算符
	`&`	取地址运算符
	`sizeof`	取大小运算符
`3`	`/`	除法运算符（算术运算符）	➡️（从左到右）
	`*`	乘法运算符（算术运算符）
	`%`	取模（取余）运算符（算术运算符）
`4`	`+`	二元加运算符（算术运算符），如：`2 + 3` 等	➡️（从左到右）
	`-`	二元减运算符（算术运算符），如：`3 - 2` 等
`5`	`<<`	左移位运算符（位运算符）	➡️（从左到右）
	`>>`	右移位运算符（位运算符）
`6`	`>`	大于运算符（比较运算符）	➡️（从左到右）
	`>=`	大于等于运算符（比较运算符）
	`<`	小于运算符（比较运算符）
	`<=`	小于等于运算符（比较运算符）
`7`	`==`	等于运算符（比较运算符）	➡️（从左到右）
	`!=`	不等于运算符（比较运算符）
`8`	`&`	按位与运算符（位运算符）	➡️（从左到右）
`9`	`^`	按位异或运算符（位运算符）	➡️（从左到右）
`10`	`\|`	按位或运算符（位运算符）	➡️（从左到右）
`11`	`&&`	逻辑与运算符（逻辑运算符）	➡️（从左到右）
`12`	`\|\|`	逻辑或运算符（逻辑运算符）	➡️（从左到右）
`13`	`?:`	三目（三元）运算符	⬅️（从右到左）
`14`	`=`	简单赋值运算符（赋值运算符）	⬅️（从右到左）
	`/=`	除后赋值运算符（赋值运算符）
	`*=`	乘后赋值运算符（赋值运算符）
	`%=`	取模后赋值运算符（赋值运算符）
	`+=`	加后赋值运算符（赋值运算符）
	`-=`	减后赋值运算符（赋值运算符）
	`<<=`	左移后赋值运算符（赋值运算符）
	`>>=`	右移后赋值运算符（赋值运算符）
	`&=`	按位与后赋值运算符（赋值运算符）
	`^=`	按位异或后赋值运算符（赋值运算符）
	`\|=`	按位或后赋值运算符（赋值运算符）
`15`	`,`	逗号运算符	➡️（从左到右）

注意

① 不要过多的依赖运算符的优先级来控制表达式的执行顺序，这样可读性太差，尽量使用小括号来控制表达式的执行顺序。
② 不要把一个表达式写得过于复杂，如果一个表达式过于复杂，则把它分成几步来完成。
③ 运算符优先级不用刻意地去记忆，总体上：一元运算符 > 算术运算符 > 关系运算符 > 逻辑运算符 > 三元运算符 > 赋值运算符 > 逗号运算符。

第二章：算术运算符（⭐）

2.1 概述

算术运算符是对数值类型的变量进行运算的，如下所示：

运算符	描述	操作数个数	组成的表达式的值	副作用
`+`	正号	1	操作数本身	❎
`-`	负号	1	操作数符号取反	❎
`+`	加号	2	两个操作数之和	❎
`-`	减号	2	两个操作数之差	❎
`*`	乘号	2	两个操作数之积	❎
`/`	除号	2	两个操作数之商	❎
`%`	取模（取余）	2	两个操作数相除的余数	❎
`++`	自增	1	操作数自增前或自增后的值	✅
`--`	自减	1	操作数自减前或自减后的值	✅

提醒

点我查看自增和自减详解

① 自增、自减运算符可以写在操作数的前面也可以写在操作数后面，不论前面还是后面，对操作数的副作用是一致的。
② 自增、自减运算符在前在后，对于表达式的值是不同的。如果运算符在前，表达式的值是操作数自增、自减之后的值；如果运算符在后，表达式的值是操作数自增、自减之前的值。
③ 变量前++：变量先自增 1 ，然后再运算；变量后++：变量先运算，然后再自增 1 。
④ 变量前--：变量先自减 1 ，然后再运算；变量后--：变量先运算，然后再自减 1 。
⑤ 对于 i++ 或 i-- ，各种编程语言的用法和支持是不同的，例如：C/C++、Java 等完全支持，Python 压根一点都不支持，Go 语言虽然支持 i++ 或 i-- ，却只支持这些操作符作为独立的语句，并且不能嵌入在其它的表达式中。

2.2 应用示例

示例：正号和负号

#include <stdio.h>

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);
    
    int x  = 12;
    int x1 = -x, x2 = +x;

    int y  = -67;
    int y1 = -y, y2 = +y;

    printf("x1=%d, x2=%d \n", x1, x2); // x1=-12, x2=12
    printf("y1=%d, y2=%d \n", y1, y2); // y1=67, y2=-67

    return 0;
}

示例：加、减、乘、除、取模

#include <stdio.h>

int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int a = 5;
    int b = 2;

    printf("%d + %d = %d\n", a, b, a + b); // 5 + 2 = 7
    printf("%d - %d = %d\n", a, b, a - b); // 5 - 2 = 3
    printf("%d × %d = %d\n", a, b, a * b); // 5 × 2 = 10
    // 除（整数之间做除法时，结果只保留整数部分而舍弃小数部分）
    printf("%d / %d = %d\n", a, b, a / b); // 5 / 2 = 2
    printf("%d %% %d = %d\n", a, b, a % b); // 5 % 2 = 1

    return 0;
}

示例：取模

#include <stdio.h>

/**
* 取模（运算结果的符号与被模数，也就是第一个操作数相同）
*/
int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int res1 = 10 % 3;
    printf("10 %% 3 = %d\n", res1); // 10 % 3 = 1

    int res2 = -10 % 3;
    printf("-10 %% 3 = %d\n", res2); // -10 % 3 = -1

    int res3 = 10 % -3;
    printf("10 %% -3 = %d\n", res3); // 10 % -3 = 1

    int res4 = -10 % -3;
    printf("-10 %% -3 = %d\n", res4); // -10 % -3 = -1

    return 0;
}

示例：自增和自减

#include <stdio.h>

int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int i1 = 10, i2 = 20;
    int i  = i1++;
    printf("i = %d\n", i); // i = 10
    printf("i1 = %d\n", i1); // i1 = 11

    i = ++i1;
    printf("i = %d\n", i); // i = 12
    printf("i1 = %d\n", i1); // i1 = 12

    i = i2--;
    printf("i = %d\n", i); // i = 20
    printf("i2 = %d\n", i2); // i2 = 19

    i = --i2;
    printf("i = %d\n", i); // i = 18
    printf("i2 = %d\n", i2); // i2 = 18

    return 0;
}

示例：

#include <stdio.h>

/*
  随意给出一个整数，打印显示它的个位数，十位数，百位数的值。
  格式如下：
    数字xxx的情况如下：
    个位数：
    十位数：
    百位数：
  例如：
    数字153的情况如下：
    个位数：3
    十位数：5
    百位数：1
 */
int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int num = 153;

    int bai = num / 100;
    int shi = num % 100 / 10;
    int ge  = num % 10;
    printf("百位为：%d \n", bai);
    printf("十位为：%d \n", shi);
    printf("个位为：%d \n", ge);

    return 0;
}

第三章：关系运算符（⭐）

3.1 概述

常见的关系运算符（比较运算符），如下所示：

运算符	描述	操作数个数	组成的表达式的值	副作用
`==`	相等	2	0 或 1	❎
`!=`	不相等	2	0 或 1	❎
`<`	小于	2	0 或 1	❎
`>`	大于	2	0 或 1	❎
`<=`	小于等于	2	0 或 1	❎
`>=`	大于等于	2	0 或 1	❎

提醒

① C 语言中，没有严格意义上的布尔类型，可以使用 0（假）或 1（真）表示布尔类型的值。
② 不要将 == 写成 =，== 是比较运算符，而 = 是赋值运算符。
③ >= 或 <=含义是：只需要满足 大于或等于、小于或等于其中一个条件，结果就返回真。

3.2 应用示例

示例：

#include <stdio.h>

int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int a = 8;
    int b = 7;

    printf("a > b 的结果是：%d \n", a > b); // a > b 的结果是：1
    printf("a >= b 的结果是：%d \n", a >= b); // a >= b 的结果是：1
    printf("a < b 的结果是：%d \n", a < b); // a < b 的结果是：0
    printf("a <= b 的结果是：%d \n", a <= b); // a <= b 的结果是：0
    printf("a == b 的结果是：%d \n", a == b); // a == b 的结果是：0
    printf("a != b 的结果是：%d \n", a != b); // a != b 的结果是：1

    return 0;
}

第四章：逻辑运算符（⭐）

4.1 概述

常见的逻辑运算符，如下所示：

运算符	描述	操作数个数	组成的表达式的值	副作用
`&&`	逻辑与	2	0 或 1	❎
`\|\|`	逻辑或	2	0 或 1	❎
`!`	逻辑非	2	0 或 1	❎

逻辑运算符提供逻辑判断功能，用于构建更复杂的表达式，如下所示：

a	b	a && b	a \|\| b	!a
1（真）	1（真）	1（真）	1（真）	0（假）
1（真）	0（假）	0（假）	1（真）	0（假）
0（假）	1（真）	0（假）	1（真）	1（真）
0（假）	0（假）	0（假）	0（假）	1（真）

提醒

点我查看逻辑运算符详解

① 对于逻辑运算符来说，任何非零值都表示真，零值表示假，如：5 || 0 返回 1 ，5 && 0 返回 0 。
② 逻辑运算符的理解：
- && 的理解就是：两边条件，同时满足。
- ||的理解就是：两边条件，二选一。
- ! 的理解就是：条件取反。
③ 短路现象：
- 对于 a && b 操作来说，当 a 为假(或 0 )时，因为 a && b 结果必定为 0，所以不再执行表达式 b。
- 对于 a || b 操作来说，当 a 为真(或非 0 )时，因为 a || b 结果必定为 1，所以不再执行表达式 b。

4.2 应用示例

示例：

#include <stdio.h>

int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int a = 0;
    int b = 0;

    printf("请输入整数a的值：");
    scanf("%d", &a);
    printf("请输入整数b的值：");
    scanf("%d", &b);

    if (a > b) {
        printf("%d > %d", a, b);
    } else if (a < b) {
        printf("%d < %d", a, b);
    } else {
        printf("%d = %d", a, b);
    }

    return 0;
}

示例：

#include <stdio.h>

// 短路现象
int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int i = 0;
    int j = 10;
    if (i && j++ > 0) {
        printf("床前明月光\n"); // 这行代码不会执行
    } else {
        printf("我叫郭德纲\n");
    }
    printf("%d \n", j); //10

    return 0;
}

示例：

#include <stdio.h>

// 短路现象

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);
    
    int i = 1;
    int j = 10;
    if (i || j++ > 0) {
        printf("床前明月光 \n");
    } else {
        printf("我叫郭德纲 \n"); // 这行代码不会被执行
    }
    printf("%d\n", j); //10

    return 0;
}

第五章：赋值运算符（⭐）

5.1 概述

常见的赋值运算符，如下所示：

运算符	描述	操作数个数	组成的表达式的值	副作用
`=`	赋值	2	左边操作数的值	✅
`+=`	相加赋值	2	左边操作数的值	✅
`-=`	相减赋值	2	左边操作数的值	✅
`*=`	相乘赋值	2	左边操作数的值	✅
`/=`	相除赋值	2	左边操作数的值	✅
`%=`	取余赋值	2	左边操作数的值	✅
`<<=`	左移赋值	2	左边操作数的值	✅
`>>=`	右移赋值	2	左边操作数的值	✅
`&=`	按位与赋值	2	左边操作数的值	✅
`^=`	按位异或赋值	2	左边操作数的值	✅
`\|=`	按位或赋值	2	左边操作数的值	✅

提醒

① 赋值运算符的第一个操作数（左值）必须是变量的形式，第二个操作数可以是任何形式的表达式。
② 赋值运算符的副作用针对第一个操作数。
③ 我们也称 =为简单赋值，而其余称为复合赋值，如：+=。

5.2 应用示例

示例：

#include <stdio.h>

int main() {
    
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int a = 3;
    a += 3; // a = a + 3
    printf("a = %d\n", a); // a = 6

    int b = 3;
    b -= 3; // b = b - 3
    printf("b = %d\n", b); // b = 0

    int c = 3;
    c *= 3; // c = c * 3
    printf("c = %d\n", c); // c = 9

    int d = 3;
    d /= 3; // d = d / 3
    printf("d = %d\n", d); // d = 1

    int e = 3;
    e %= 3; // e = e % 3
    printf("e = %d\n", e); // e = 0

    return 0;
}

第六章：位运算符

6.1 概述

C 语言提供了一些位运算符，能够让我们操作二进制位（bit）。
常见的位运算符，如下所示。

运算符	描述	操作数个数	运算规则	副作用
`&`	按位与	2	两个二进制位都为 1 ，结果为 1 ，否则为 0	❎
`\|`	按位或	2	两个二进制位只要有一个为 1（包含两个都为 1 的情况），结果为 1 ，否则为 0	❎
`^`	按位异或	2	两个二进制位一个为 0 ，一个为 1 ，结果为 1，否则为 0	❎
`~`	按位取反	2	将每一个二进制位变成相反值，即：0 变成 1 ， 1 变成 0	❎
`<<`	左移	2	将一个数的各个二进制位全部左移指定的位数，左边的二进制位丢弃，右边补 0	❎
`>>`	右移	2	将一个数的各个二进制位全部右移指定的位数，正数左补 0，负数左补 1，右边丢弃	❎

提醒

① 操作数在进行位运算的时候，以它的补码形式计算！！！
② C 语言中的位运算符，分为如下的两类：
- 按位运算符：按位与（&）、按位或（|）、按位异或（^）、按位取反（~）。
- 移位运算符：左移（<<）、右移（>>）。

6.2 输出二进制位

在 C 语言中，printf 是没有提供输出二进制位的格式占位符的；但是，我们可以手动实现，以方便后期操作。

提醒

① 在 C23 标准之前，printf 和 scanf 都不支持二进制整数。
② 在 C23 标准中，printf 和 scanf 开始支持二进制整数，其对应的格式占位符是 %b。

示例：

#include <stdio.h>

/**
 * 获取指定整数的二进制表示
 * @param num 整数
 * @return 二进制表示的字符串，不包括前导的 '0b' 字符
 */
char *getBinary(int num) {
    static char binaryString[33 + (sizeof(int) * 8 / 8)];
    int         i, j;

    for (i = sizeof(num) * 8 - 1, j = 0; i >= 0; i--, j++) {
        const int bit   = (num >> i) & 1;
        binaryString[j] = bit + '0';
        // 每 8 位后添加一个空格
        if ((i % 8) == 0 && i != 0) {
            binaryString[++j] = ' ';
        }
    }

    binaryString[j] = '\0';
    return binaryString;
}

int main() {
    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);
    
    int a = 17;
    int b = -12;

    printf("整数 %d 的二进制表示：%s \n", a, getBinary(a));
    printf("整数 %d 的二进制表示：%s \n", b, getBinary(b));

    return 0;
}

6.3 按位与运算符

6.3.1 概述

按位与 & 的运算规则是：如果二进制对应的位上都是 1 才是 1 ，否则为 0 ，即：
- 1 & 1 的结果是 1 。
- 1 & 0 的结果是 0 。
- 0 & 1 的结果是 0 。
- 0 & 0 的结果是 0 。

6.3.2 理解

① 按位与背后就是电路设计中的与门电路，如下所示：

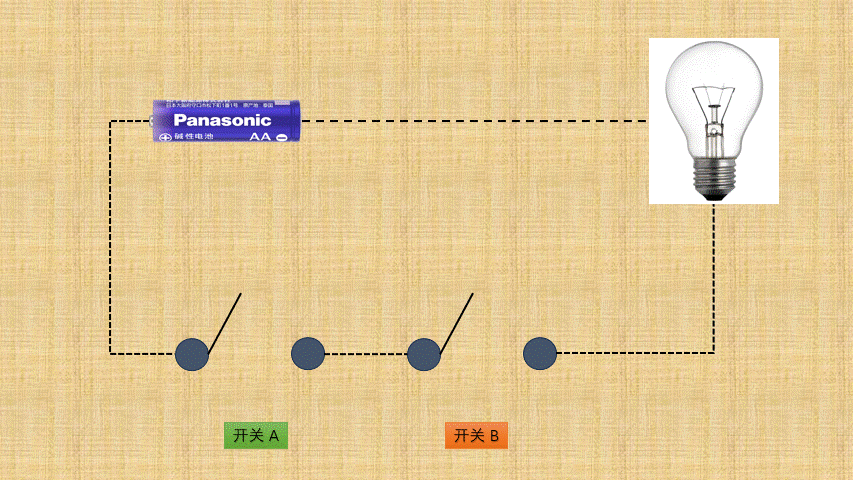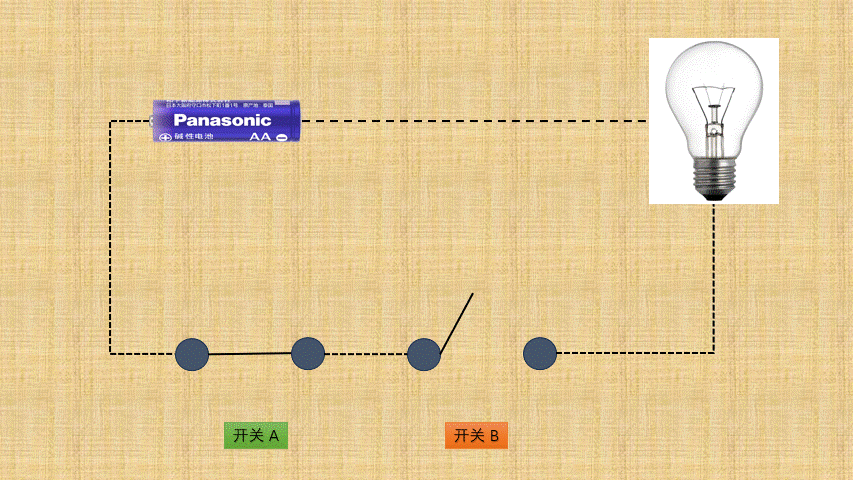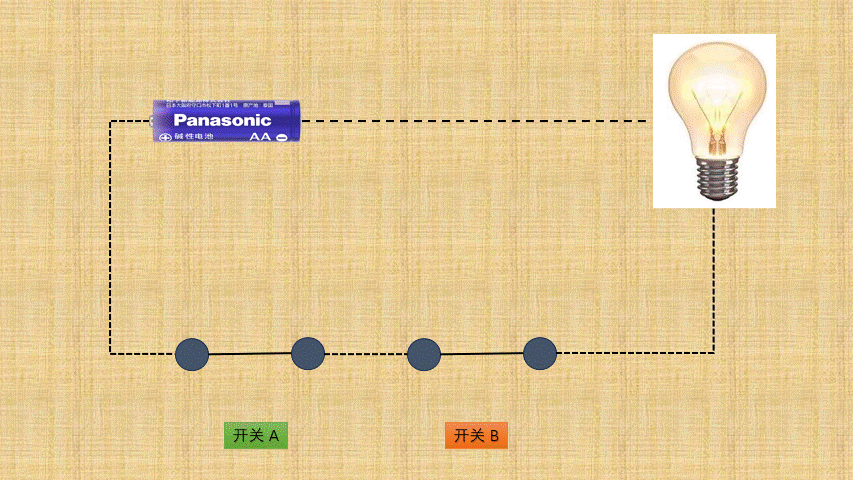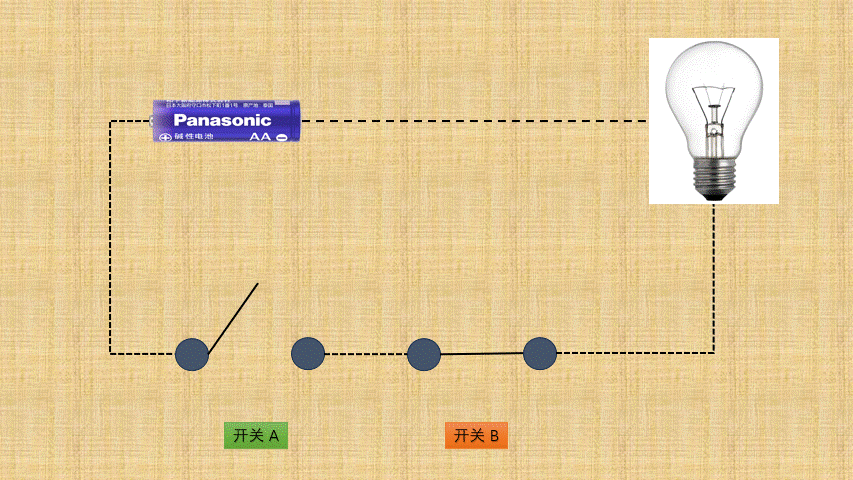
② 如果将开关的连通和断开称为输入端，而灯泡的连通（亮）和断开（暗）称为输出端，并将整个电路都封装到一个图形中；那么，与门电路就是这样的，如下所示：

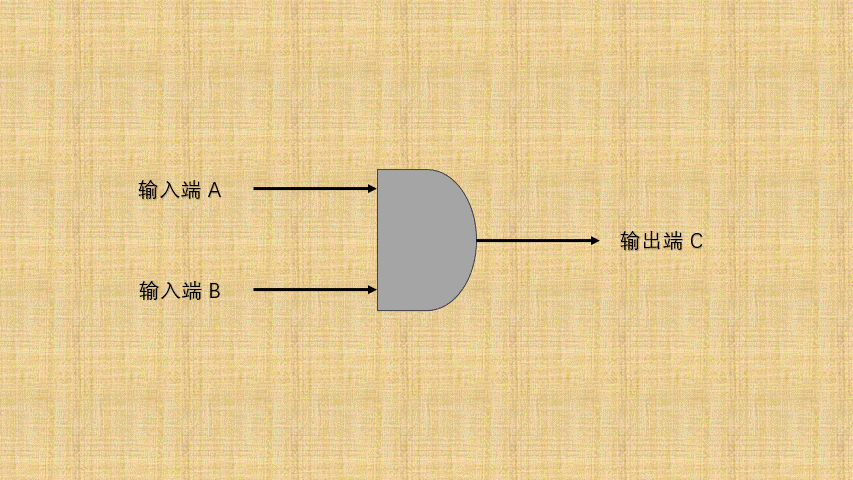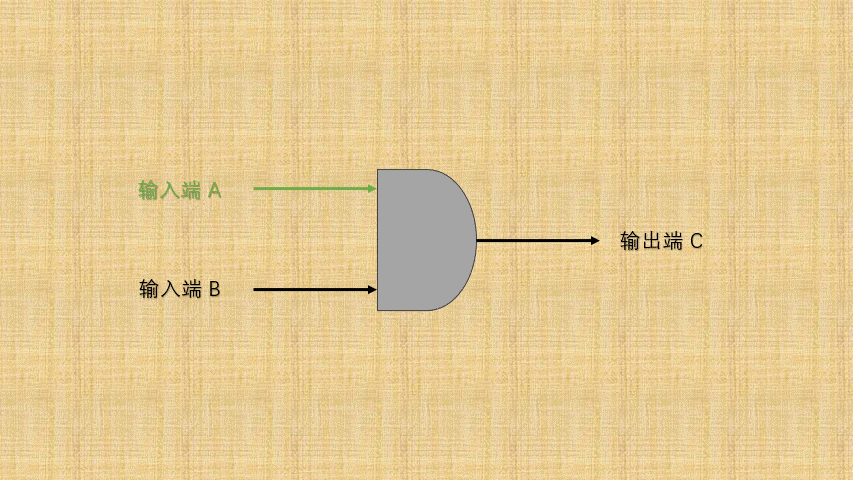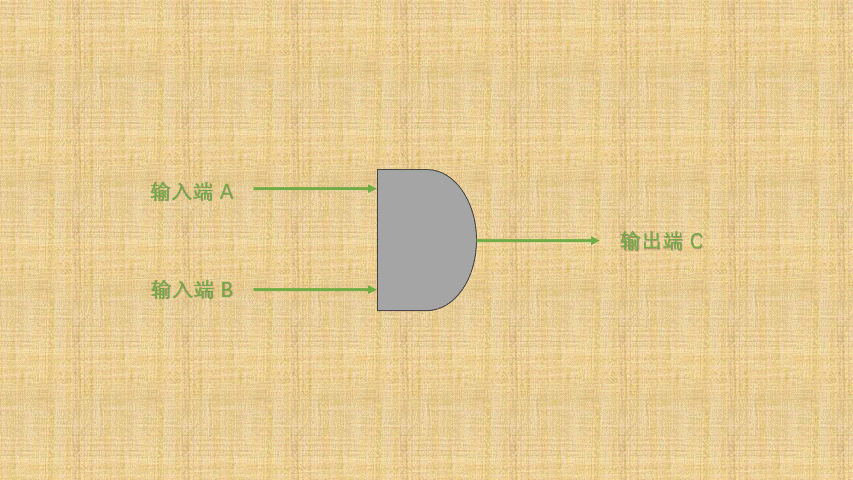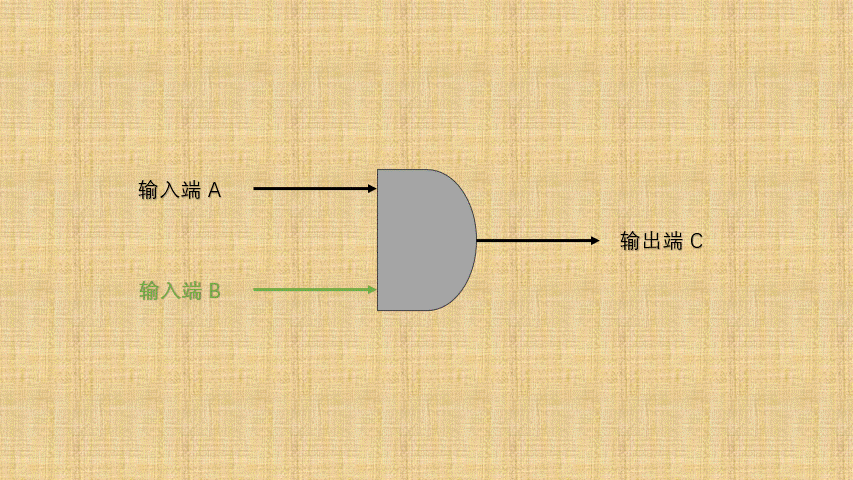
③ 可以将电路的连通使用数字 1 表示，电路的断开使用数字 0 那么，与门电路就是这样的，如下所示：

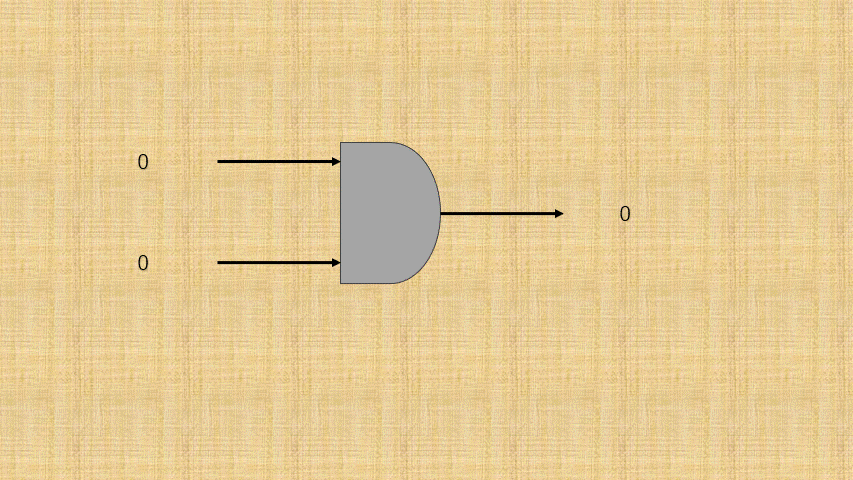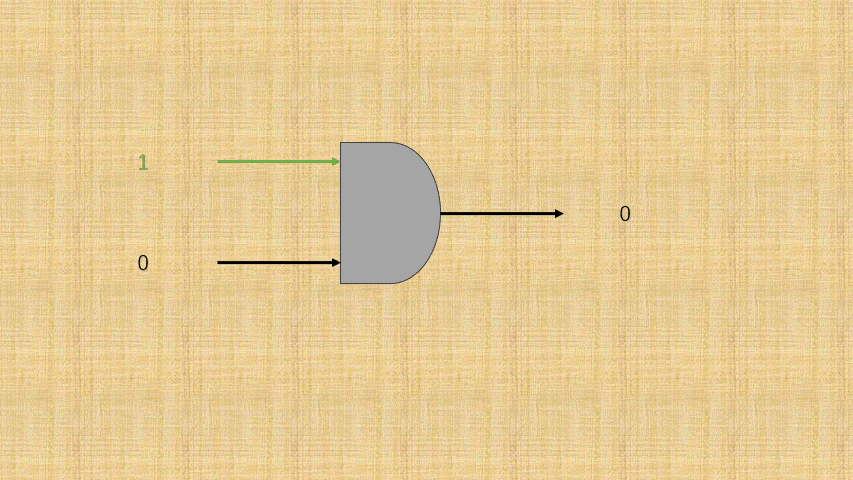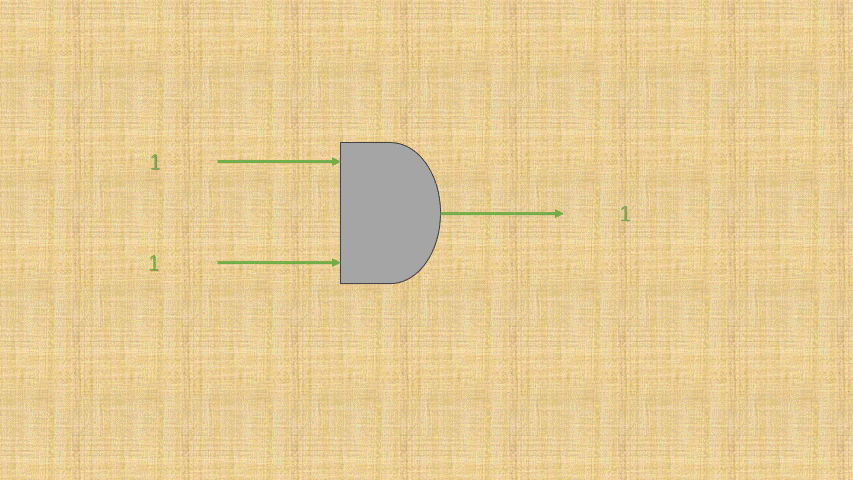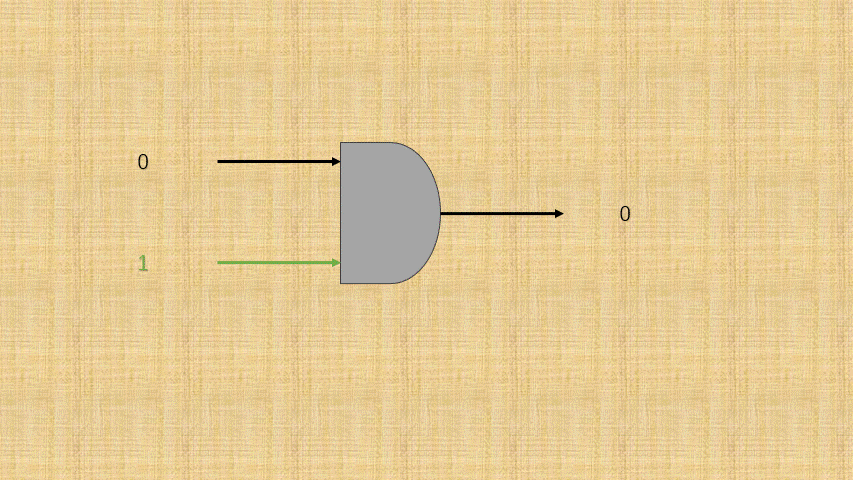
④ 位与运算就类似数学中的交集，如下所示：

6.3.3 应用示例

示例：9 & 7 = 1

示例：-9 & 7 = 7

6.4 按位或运算符

6.4.1 概述

按位或 | 的运算规则是：如果二进制对应的位上只要有 1 就是 1 ，否则为 0 ，即：
- 1 | 1 的结果是 1 。
- 1 | 0 的结果是 1 。
- 0 | 1 的结果是 1 。
- 0 | 0 的结果是 0 。

6.4.2 理解

① 按位或背后就是电路设计中的或门电路，如下所示：

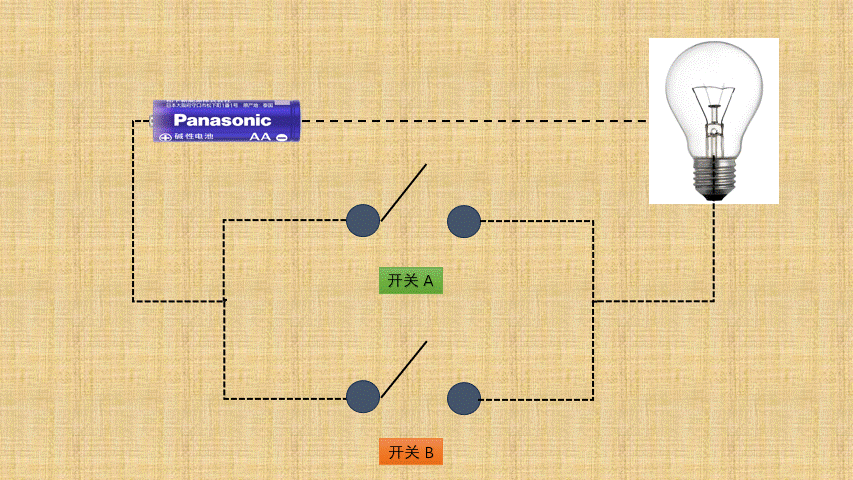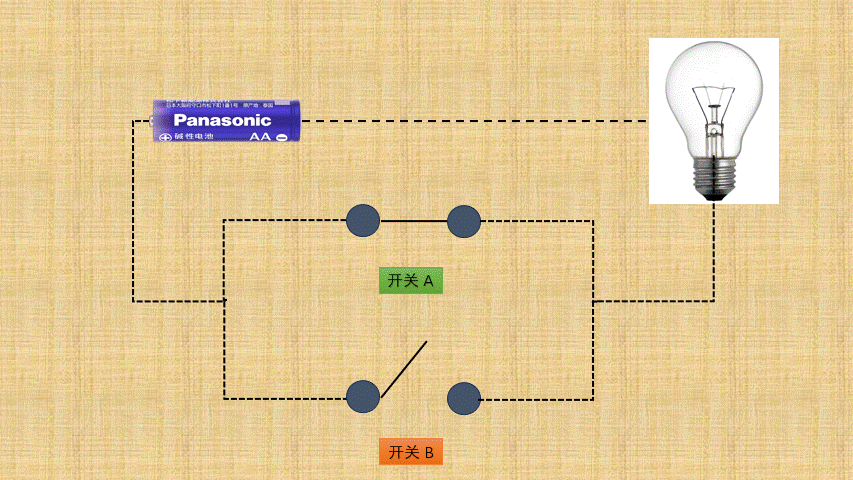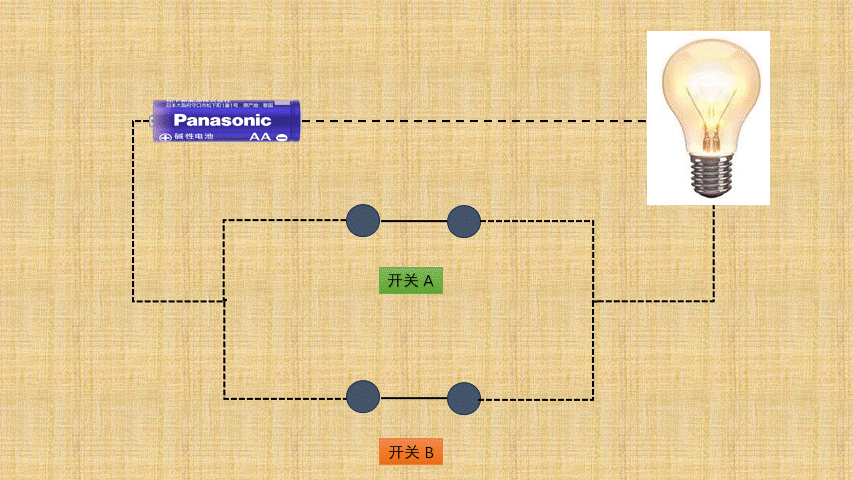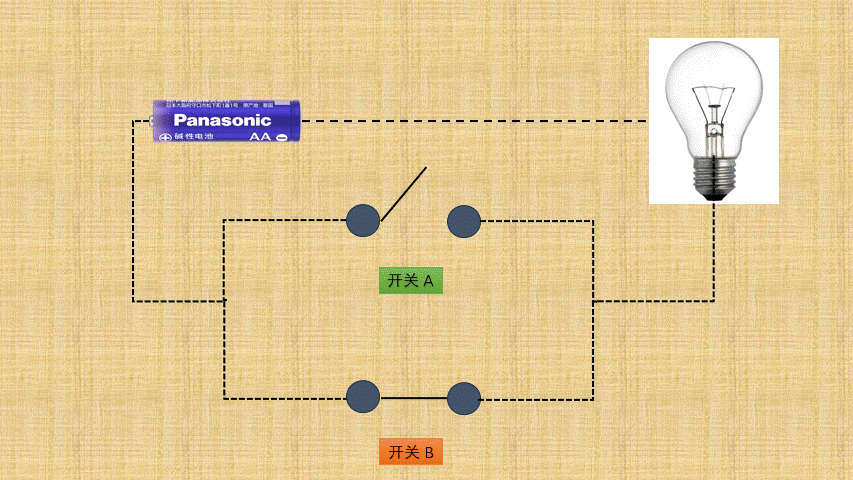
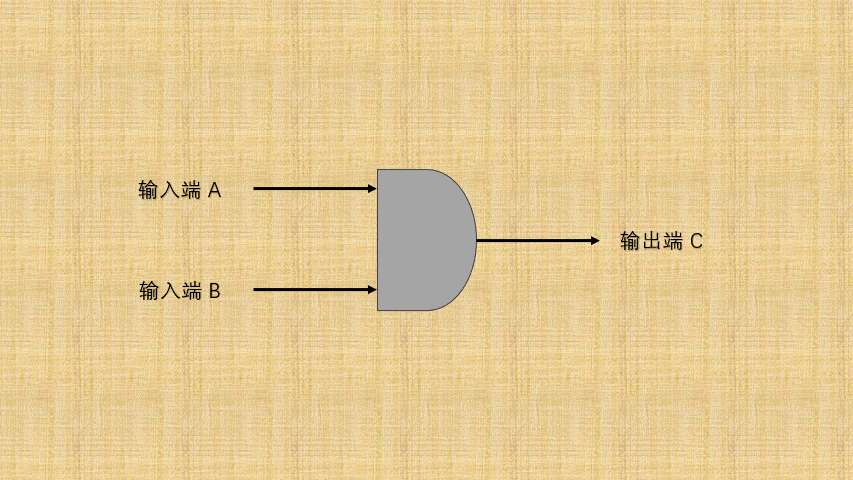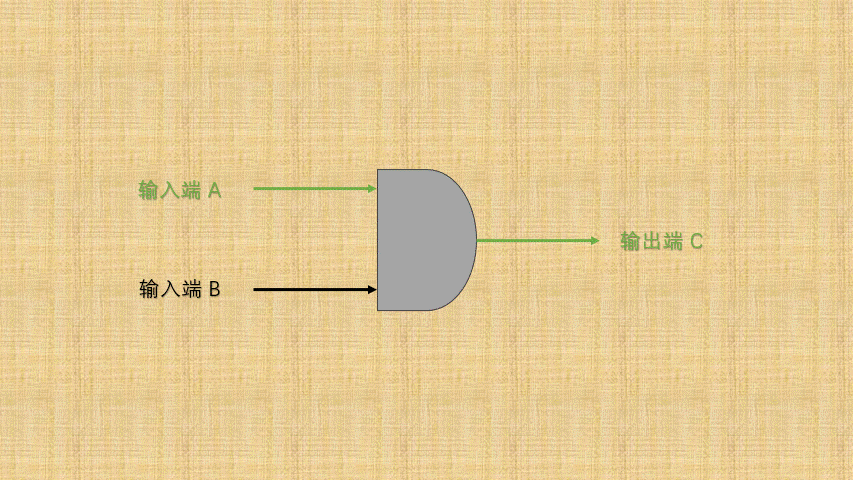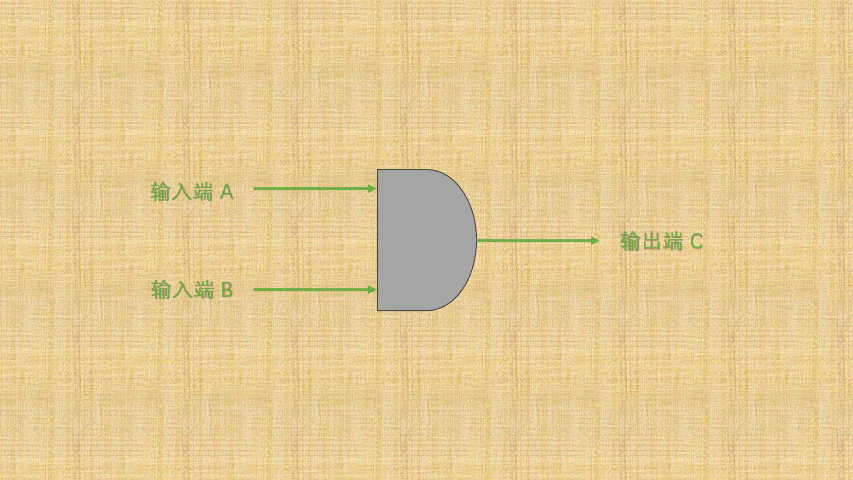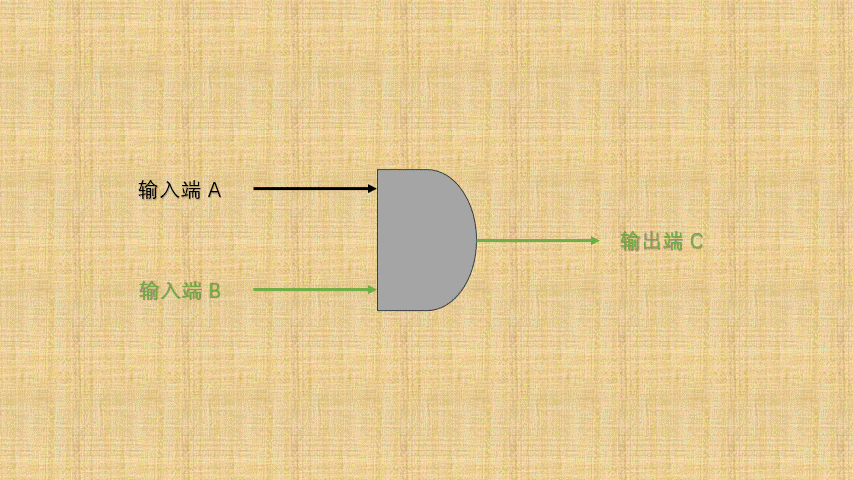
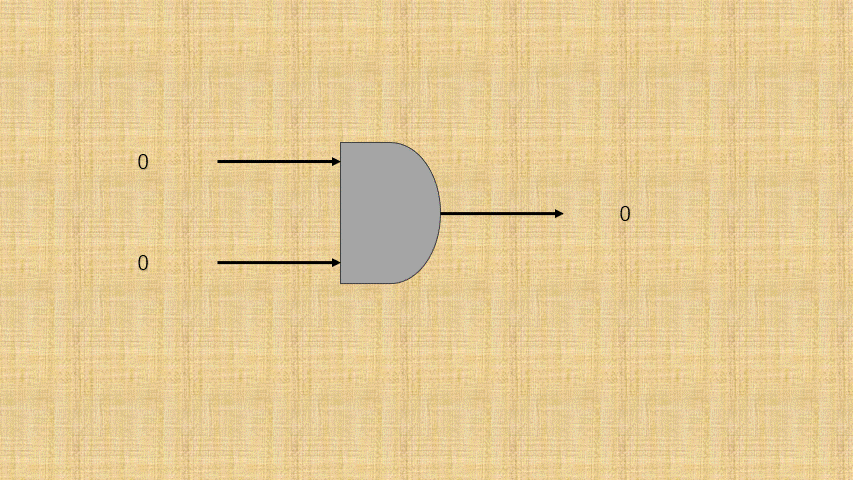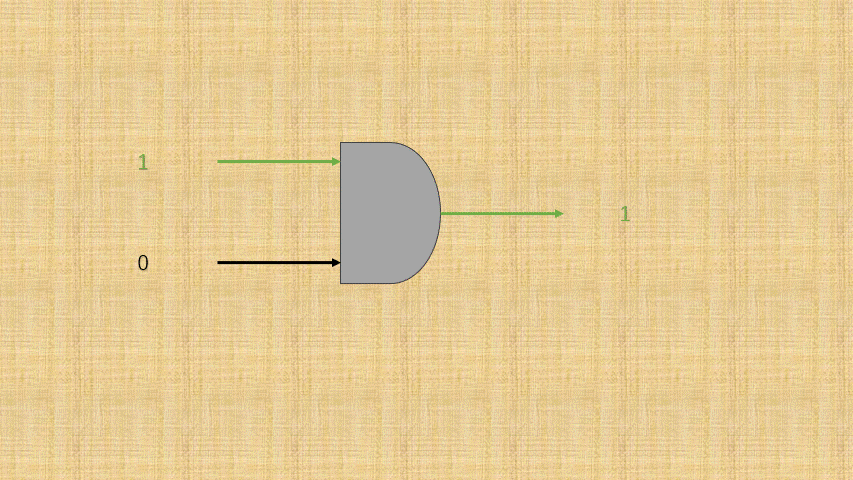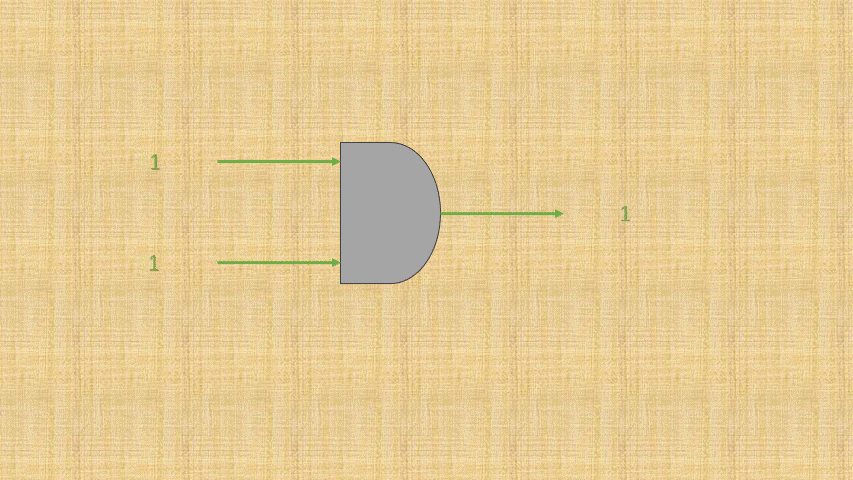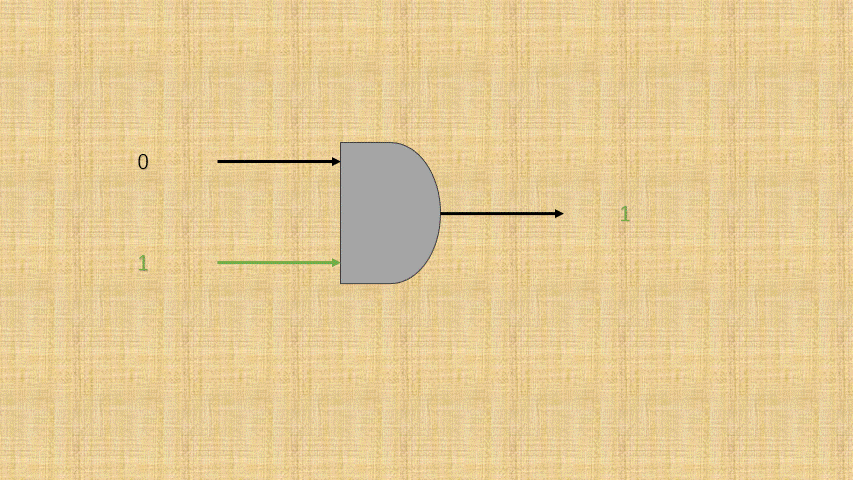
② 如果将开关的连通和断开称为输入端，而灯泡的连通（亮）和断开（暗）称为输出端，并将整个电路都封装到一个图形中；那么，或门电路就是这样的，如下所示：

③ 可以将电路的连通使用数字 1 表示，电路的断开使用数字 0 表示；那么，或门电路就是这样的，如下所示：

④ 位或运算就类似数学中的并集，如下所示：

6.4.3 应用示例

示例：9 | 7 = 15

示例：-9 | 7 = -9

6.5 按位异或运算符

6.5.1 概述

按位异或 ^ 的运算规则是：如果二进制对应的位上一个为 1 一个为 0 就为 1 ，否则为 0 ，即：
- 1 ^ 1 的结果是 0 。
- 1 ^ 0 的结果是 1 。
- 0 ^ 1 的结果是 1 。
- 0 ^ 0 的结果是 0 。

提醒

按位异或的应用场景：

① 交换两个数值：异或操作可以在不使用临时变量的情况下交换两个变量的值。
② 加密或解密：异或操作用于简单的加密和解密算法。
③ 错误检测和校正：异或操作可以用于奇偶校验位的计算和检测错误（RAID-3 以及以上）。
……

提醒

按位异或的一些特性：

① 恒等性（异或 0 等于本身）：a ^ 0 = a
② 自反性（归零性）（异或自己等于 0）：a ^ a = 0 。
③ 交换性：a ^ b = b ^ a。
④ 结合性： (a ^ b) ^ c = a ^ (b ^ c) 。
⑤ 对合性：a ^ b ^ b = a ^ 0 = a 。

6.5.2 理解

① 按位异或背后就是电路设计中的异或门电路，如下所示：

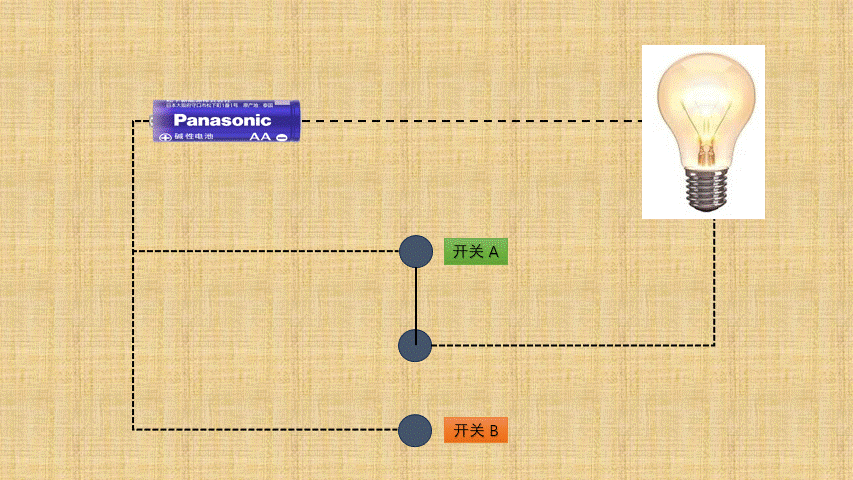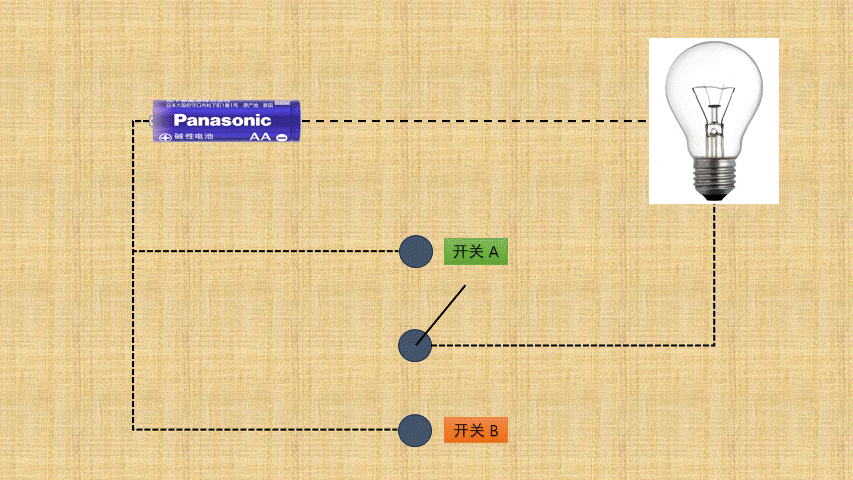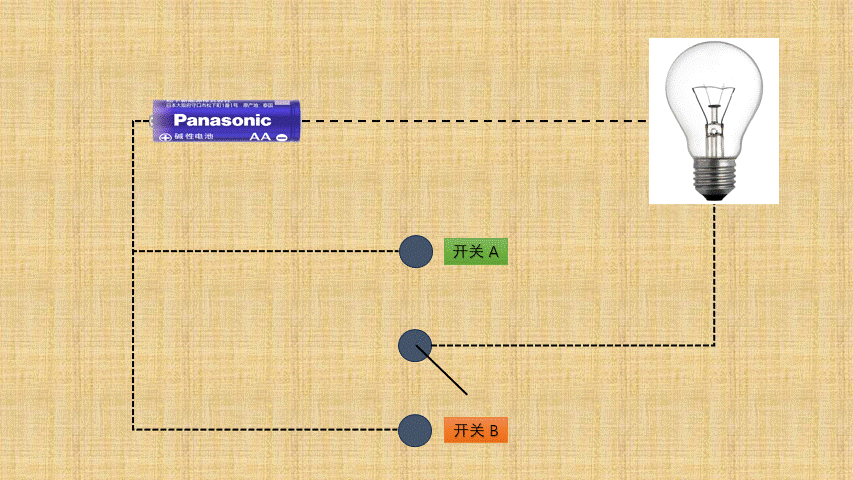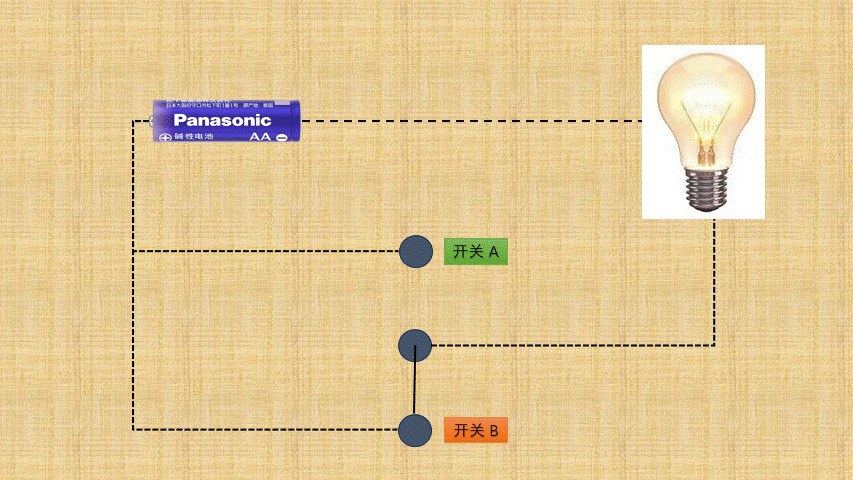
② 如果将开关的连通和断开称为输入端，而灯泡的连通（亮）和断开（暗）称为输出端，并将整个电路都封装到一个图形中；那么，异或门电路就是这样的，如下所示：

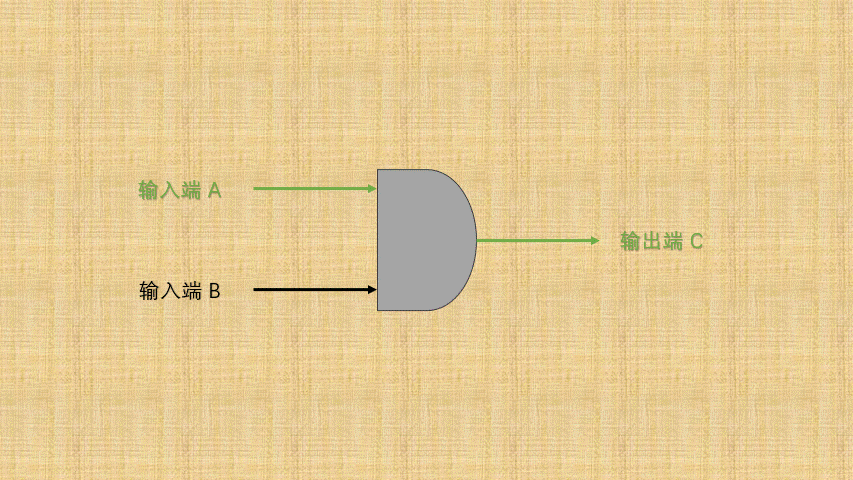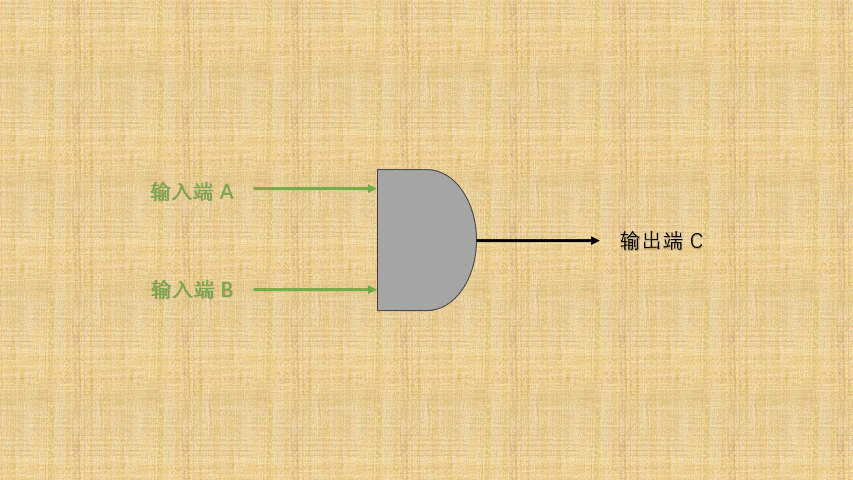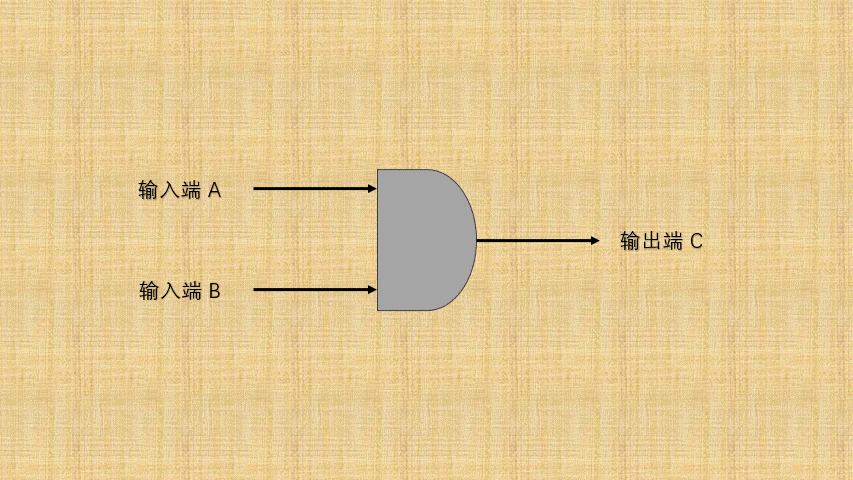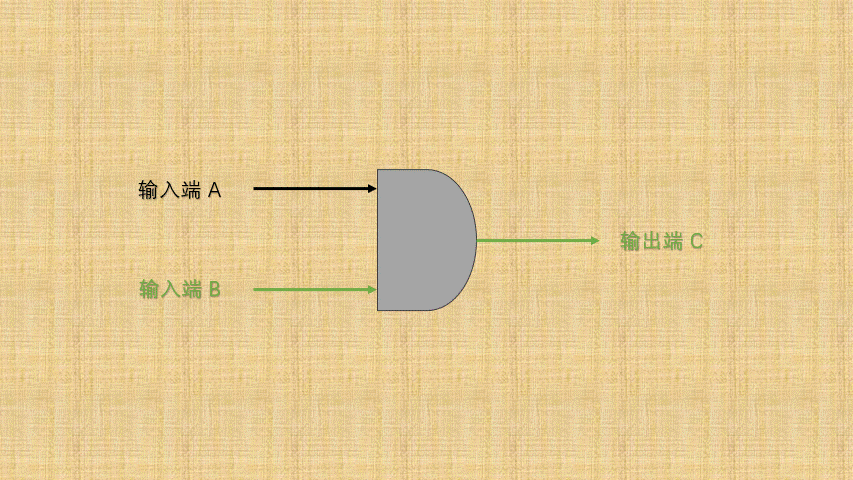
③ 可以将电路的连通使用数字 1 表示，电路的断开使用数字 0 表示；那么，异或门电路就是这样的，如下所示：

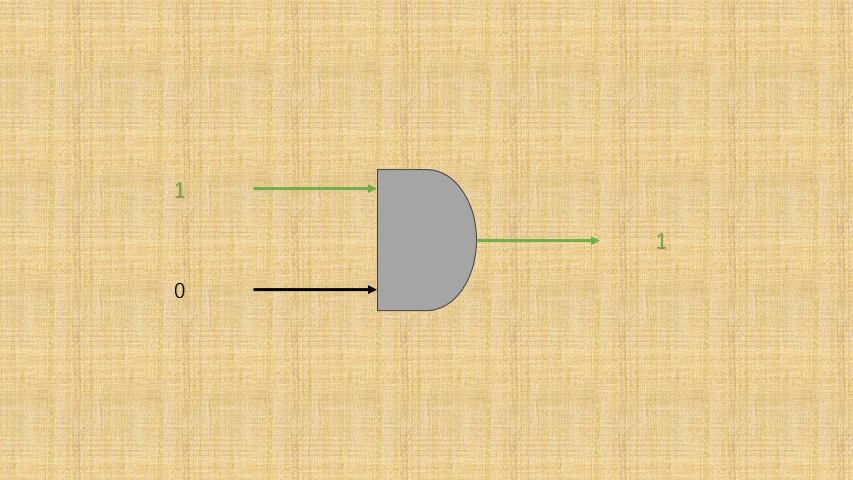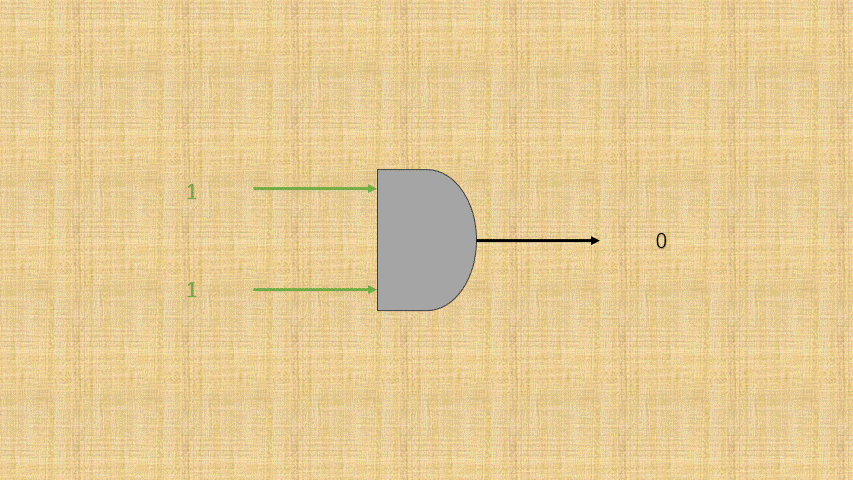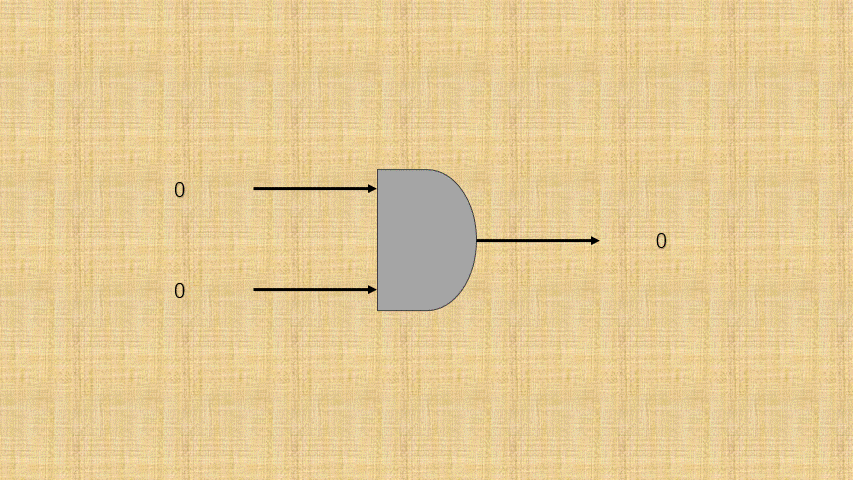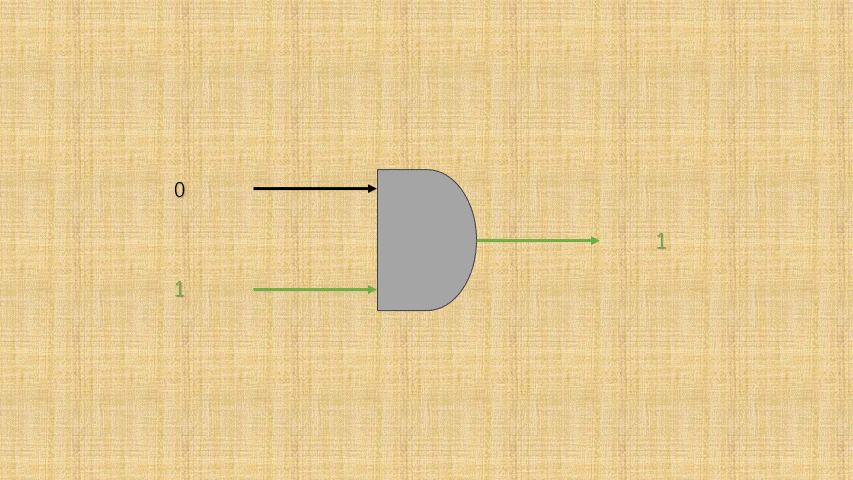
④ 位或运算就类似数学中的差集，如下所示：

6.5.3 应用示例

示例：9 ^ 7 = 14

示例：-9 ^ 7 = -16

6.6 按位取反运算符

6.6.1 概述

按位取反（~）运算规则：如果二进制对应的位上是 1，结果为 0；如果是 0 ，则结果为 1 。
- ~0 的结果是 1 。
- ~1 的结果是 0 。

6.6.2 应用示例

示例：~9 = -10

示例：~-9 = 8

6.7 移位运算符

6.7.1 左移运算符

在一定范围内，数据每向左移动一位，相当于原数据 × 2（正数、负数都适用）。
示例：3 << 4 = 48 （3 × 2^4）

示例：-3 << 4 = -48 （-3 × 2 ^4）

6.7.2 右移运算符

在一定范围内，数据每向右移动一位，相当于原数据 ÷ 2（正数、负数都适用）。

提醒

① 如果不能整除，则向下取整。
② 右移运算符最好只用于无符号整数，不要用于负数：因为不同系统对于右移后如何处理负数的符号位，有不同的做法，可能会得到不一样的结果。

示例：69 >> 4 = 4 （69 ÷ 2^4 ）

示例：-69 >> 4 = -5 （-69 ÷ 2^4 ）

6.8 异或运算符的特性

6.8.1 恒等性

如果一个数和 0 进行异或运算，结果还是这个数本身，即：a ^ 0 = a 。
示例：1101 0010 ^ 0 = 1101 0010

6.8.2 自反性（归零性）

如果一个数和其本身进行异或运算，结果是 0 ，即：a ^ a = 0。
示例：1101 0010 ^ 1101 0010 = 0000 0000

6.8.3 交换性

对于任意的两个数 a 和 b 在进行异或运算的时候，交换顺序并不影响结果，即：a ^ b = b ^ a 。
示例：1101 0010 ^ 1001 1010 = 0100 1000

示例：1001 1010 ^ 1101 0010 = 0100 1000

6.8.4 结合性

对于任意的三个数a、b和c在进行异或运算的时候，交换顺序并不影响结果，即：(a^b)^c = a^(b^c) 。
示例：1101 0010 ^ 0100 1000 ^ 1011 0010 = 0010 1000

1101 0010 ^ 0100 1000 ^ 1011 0010 = 0010 1000

示例：0100 1000 ^ 1011 0010 ^ 1101 0010 = 0010 1000

0100 1000 ^ 1011 0010 ^ 1101 0010 = 0010 1000

6.8.5 对合性

对于任意的两个数a和b，进行两次异或运算，结果会恢复到原来的数值，即：a^b^b = a 。

提醒

① a ^ b ^ b = a --> a ^ b ^ b --> a ^ (b ^ b) --> a ^ 0 --> a。
② a ^ b ^ a = b --> b ^ a ^ a --> b ^ (a ^ a) --> b ^ 0 --> b。

重要

异或运算可以很好地应用于是加密算法和数据校验等领域，我们可以利用异或运算的对合性对数据进行加密和解密，如：在加密过程中，使用一个密钥对数据进行异或运算；再使用相同的密钥对加密之后的结果进行异或运算，就能够恢复原数据（对称加密）。

示例：1011 0111 ^ 0101 1000 ^ 0101 1000 = 1011 0111

1011 0111 ^ 0101 1000 ^ 0101 1000 = 1011 0111

6.9 经典面试题

6.9.1 面试题 1

需求：判断一个整数是否为奇数？

提醒

① 从数学角度讲，如果一个数 num ，满足 num % 2 != 0 的条件，就说明该数是一个奇数；否则，该数是一个偶数。
② 从计算机底层角度讲，一个有符号整数，在计算机底层存储的二进制是 $b_{n - 1} b_{n - 2} \dots b_{1} b_{0}$ ；那么，其对应的十进制是 $(- 1)^{b_{n - 1}} \cdot b_{n - 1} \cdot 2^{n - 1} + b_{n - 2} \cdot 2^{n - 2} + b_{n - 3} \cdot 2^{n - 3} + \dots + b_{1} \cdot 2^{1} + b_{0} \cdot 2^{0}$ ，如果对应的十进制最后一位 $b_{0} \cdot 2^{0}$ 是奇数，则说明该数为奇数（和 0x1 进行按位与运算）；否则，该数是一个偶数。

示例：数学角度方式

#include <stdio.h>

/**
 * 判断一个数是否为奇数
 *
 * @param num
 * @return
 */
bool isOdd(int num) {
    return num % 2 != 0;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int num = -10;

    printf("%d 是奇数：%s\n", num, isOdd(num) ? "true" : "false");

    num = -3;

    printf("%d 是奇数：%s\n", num, isOdd(num) ? "true" : "false");

    return 0;
}

示例：计算机底层角度方式

#include <stdio.h>

/**
 * 判断一个数是否为奇数
 *
 * @param num
 * @return
 */
bool isOdd(int num) {
    return (num & 0x1) == 1;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int num = -10;

    printf("%d 是奇数：%s\n", num, isOdd(num) ? "true" : "false");

    num = -3;

    printf("%d 是奇数：%s\n", num, isOdd(num) ? "true" : "false");

    return 0;
}

6.9.2 面试题 2

需求：如何判断一个非 0 的整数是否是 2 的幂（1、2、4、8、16）？

提醒

① 从数学角度讲，如果一个整数 num 可以被 2 整数，就让 num 除以 2 （假设 num = 2 ，那么 num /= 2 ，则 num = 1）...，如果最后 num = 1 ，则说明整数 num 是 2 的幂；否则，该整数 num 不是 2 的幂。
② 从计算机底层角度讲，如果一个整数 num 是 2 的幂，那么它的二进制表示中只有一个是 1 ，其余都是 0 ，如：1（0001）、2（0010）、4（0100）、8（1000），我们可以得到一个规律：如果 num 和 num - 1 进行按位与运算，结果为 0 ；那么，该整数 num 就是 2 的幂；否则，该整数 num 不是 2 的幂。

示例：数学角度方式

#include <stdio.h>

/**
 * 判断一个非 0 的整数是否是 2 的幂
 *
 * @param num
 * @return
 */
bool isPowOfTwo(int num) {
    if (num <= 0) {
        return false;
    }
    while (num % 2 == 0) {
        num /= 2;
    }
    return num == 1;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int num = 1;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");

    num = 2;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");

    num = 3;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");

    num = 4;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");


    return 0;
}

示例：计算机底层角度方式

#include <stdio.h>

/**
 * 判断一个非 0 的整数是否是 2 的幂
 *
 * @param num
 * @return
 */
bool isPowOfTwo(int num) {
    if (num <= 0) {
        return false;
    }

    return (num & (num - 1)) == 0;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int num = 1;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");

    num = 2;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");

    num = 3;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");

    num = 4;
    printf("%d 是 2 的幂：%s\n", num, isPowOfTwo(num) ? "true" : "false");


    return 0;
}

6.9.3 面试题 3

需求：给定一个值不为 0 的整数，请找出值为 1 的最低有效位（Least Significant Bit，LSB）。

提醒

① 假设该值是 24 ，其对应的二进制是 0001 1000，则值为 1 的最低有效位是 2^3，即：8 。
② x + (-x) = 10000 ... 0000 。其中，x 是自然数，如：1、2 等；10000 ... 0000 中有 n 个 0 ，1 会溢出，会被丢弃，即：

点我查看

txt

问：如果一个有符号数，在计算机中的存储是 1101 0100（补码） ，求其相反数的二进制表示？
答：从右往左数，第一个为 1 的数，保留下来（100），其余按位取反，即：0010 1100

③ x & -x 的结果就是最低有效位，即：

点我查看

txt

 x = 1101 0100
-x = 0010 1100
 & -------------
     0000 0100

示例：

#include <stdio.h>

/**
 * 要找出一个不为 0 的整数值为 1 的最低有效位
 * @param num
 * @return
 */
int findLowestSetBit(int num) {
    int x = 0x1; // 1 2 4 8 ...
    while ((num & x) == 0) {
        x <<= 1;
    }
    return x;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int num = 24;

    // 24 的最低有效位是：8
    printf("24 的最低有效位是：%d\n", findLowestSetBit(num));

    return 0;
}

示例：

#include <stdio.h>

/**
 * 要找出一个不为 0 的整数值为 1 的最低有效位
 * @param num
 * @return
 */
int findLowestSetBit(int num) {
    return num & -num;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int num = 24;

    // 24 的最低有效位是：8
    printf("24 的最低有效位是：%d\n", findLowestSetBit(num));

    return 0;
}

6.9.4 面试题 4

需求：给定两个不同的整数 a 和 b ，请交换它们两个的值。

提醒

① 借用第三个变量充当临时容器，来实现需求。
② 借用按位异或运算符的对合性，即：a^b^b = a 。

示例：

#include <stdio.h>

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int a = 10;
    int b = 20;

    // a = 10, b = 20
    printf("a = %d, b = %d\n", a, b);

    int temp = a;
    a = b;
    b = temp;

    // a = 20, b = 10
    printf("a = %d, b = %d\n", a, b);

    return 0;
}

示例：

#include <stdio.h>

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int a = 10;
    int b = 20;

    // a = 10, b = 20
    printf("a = %d, b = %d\n", a, b);

    a = a ^ b; // a = a0 ^ b0
    b = a ^ b; // b = a0 ^ b0 ^ b0 = a0
    a = a ^ b; // a = a0 ^ b0 ^ a0 = b0

    // a = 20, b = 10
    printf("a = %d, b = %d\n", a, b);

    return 0;
}

6.9.5 面试题 5

需求：给出一个非空整数数组 nums，除了某个元素只出现 1 次以外，其余每个元素均出现 2 次，请找出那个只出现 1 次的元素。

提醒

① 如果 nums = [1,4,2,1,2]，那么只出现 1 次的元素就是 4 。
② 借用按位异或运算符的恒等性，即：a ^ 0 = a，和按位异或运算符的自反性（归零性），即：a ^ a = 0。

示例：

#include <stdio.h>

/**
 * 任何数与 0 异或等于其本身，任何数与其自身异或等于 0 。
 * 因此，数组中成对出现的数字将通过异或运算抵消为 0 ，
 * 最终剩下的结果就是唯一出现一次的数字。
 * @param arr
 * @param len
 * @return
 */
int findOnly(const int arr[], size_t len) {

    int singleNum = 0;

    for (int i = 0; i < len; ++i) {
        singleNum ^= arr[i];
    }

    return singleNum;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int nums[] = {1, 4, 2, 1, 2};

    int num = findOnly(nums, sizeof(nums) / sizeof(int));

    printf("%d\n", num); // 4

    return 0;
}

6.9.6 面试题 6

需求：给出一个非空整数数组 nums；其中，恰好有两个元素只出现 1 次，其余所有元素均出现 2 次，请找出只出现 1 次的两个元素。

提醒

① 如果 nums = [1,2,1,3,2,5]，那么只出现 2 次的元素就是 [3,5] 或 [5,3] 。
② 思路（假设这两个元素是 a 和 b）：
- 核心思路就是分区：
txt
```
a(3),2,2...
b(5),1,1...
```
1
2
- 对数组中的所有元素进行异或运算（xor），得到两个只出现一次的元素的异或结果（成对出现的元素的异或结果为 0 ，所以最终的结果就是这两个只出现一次的元素的异或结果），即：a ^ b = xor（不为 0）。
- 因为 a 和 b 不同，那么 a 和 b 的二进制补码，至少有一位是不同的，即：a ^ b 至少有一位是 1 （xor 至少有一位是 1）。
- 根据面试题 3 LSB 找出值为 1 的最低有效位，即：LSB = xor & (-xor)，并且 LSB 是 2 的幂（a 和 b 在这一位上是不同的，也就意味着根据 LSB 可以将所有元素分区）。

示例：

#include <stdio.h>

/**
 * 要找出一个不为 0 的整数值为 1 的最低有效位
 * @param num
 * @return
 */
int findLowestSetBit(int num) {
    return num & -num;
}

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int nums[] = {1, 2, 1, 3, 2, 5};

    int len = sizeof(nums) / sizeof(int);

    int xor = 0;
    for (int i = 0; i < len; ++i) {
        xor ^= nums[i];
    }

    // xor = a ^ b
    printf("xor = %d\n", xor);

    // a 和 b 在这一位上是不同的
    int lsb = findLowestSetBit(xor);

    printf("lsb = %d\n", lsb);

    // 根据这一位将所有元素分类
    int a = 0, b = 0;
    for (int i = 0; i < len; ++i) {
        if (nums[i] & lsb) { // 1
            a ^= nums[i];
        } else { // 0
            b ^= nums[i];
        }
    }

    // a = 3, b = 5
    printf("a = %d, b = %d\n", a, b);

    return 0;
}

第七章：三元运算符（⭐）

7.1 概述

语法：

条件表达式 ? 表达式1 : 表达式2 ;

提醒

① 如果条件表达式为非 0 （真），则整个表达式的值是表达式 1 。
② 如果条件表达式为 0 （假），则整个表达式的值是表达式 2 。

7.2 应用示例

示例：

#include <stdio.h>

int main() {

    // 禁用 stdout 缓冲区
    setbuf(stdout, nullptr);

    int m   = 110;
    int n   = 20;
    int max = m >= n ? m : n;
    // 110 和 20 中的最大值是：110
    printf("%d 和 %d 中的最大值是：%d\n", m, n, max);

    return 0;
}

分享此页面

第一章：前言 ​

1.1 运算符、表达式和操作数 ​

1.2 运算符的分类 ​

1.3 优先级和结合性（⭐） ​

1.3.1 概述 ​

1.3.2 优先级和结合性 ​

第二章：算术运算符（⭐） ​

2.1 概述 ​

2.2 应用示例 ​

第三章：关系运算符（⭐） ​

3.1 概述 ​

3.2 应用示例 ​

第四章：逻辑运算符（⭐） ​

4.1 概述 ​

4.2 应用示例 ​

第五章：赋值运算符（⭐） ​

5.1 概述 ​

5.2 应用示例 ​

第六章：位运算符 ​

6.1 概述 ​

6.2 输出二进制位 ​

6.3 按位与运算符 ​

6.3.1 概述 ​

6.3.2 理解 ​

6.3.3 应用示例 ​

6.4 按位或运算符 ​

6.4.1 概述 ​

6.4.2 理解 ​

6.4.3 应用示例 ​

6.5 按位异或运算符 ​

6.5.1 概述 ​

6.5.2 理解 ​

6.5.3 应用示例 ​

6.6 按位取反运算符 ​

6.6.1 概述 ​

6.6.2 应用示例 ​

6.7 移位运算符 ​

6.7.1 左移运算符 ​

6.7.2 右移运算符 ​

6.8 异或运算符的特性 ​

6.8.1 恒等性 ​

6.8.2 自反性（归零性） ​

6.8.3 交换性 ​

6.8.4 结合性 ​

6.8.5 对合性 ​

6.9 经典面试题 ​

6.9.1 面试题 1 ​

6.9.2 面试题 2 ​

6.9.3 面试题 3 ​

6.9.4 面试题 4 ​

6.9.5 面试题 5 ​

6.9.6 面试题 6 ​

第七章：三元运算符（⭐） ​

7.1 概述 ​

7.2 应用示例 ​

第一章：前言

1.1 运算符、表达式和操作数

1.2 运算符的分类

1.3 优先级和结合性（⭐）

1.3.1 概述

1.3.2 优先级和结合性

第二章：算术运算符（⭐）

2.1 概述

2.2 应用示例

第三章：关系运算符（⭐）

3.1 概述

3.2 应用示例

第四章：逻辑运算符（⭐）

4.1 概述

4.2 应用示例

第五章：赋值运算符（⭐）

5.1 概述

5.2 应用示例

第六章：位运算符

6.1 概述

6.2 输出二进制位

6.3 按位与运算符

6.3.1 概述

6.3.2 理解

6.3.3 应用示例

6.4 按位或运算符

6.4.1 概述

6.4.2 理解

6.4.3 应用示例

6.5 按位异或运算符

6.5.1 概述

6.5.2 理解

6.5.3 应用示例

6.6 按位取反运算符

6.6.1 概述

6.6.2 应用示例

6.7 移位运算符

6.7.1 左移运算符

6.7.2 右移运算符

6.8 异或运算符的特性

6.8.1 恒等性

6.8.2 自反性（归零性）

6.8.3 交换性

6.8.4 结合性

6.8.5 对合性

6.9 经典面试题

6.9.1 面试题 1

6.9.2 面试题 2

6.9.3 面试题 3

6.9.4 面试题 4

6.9.5 面试题 5

6.9.6 面试题 6

第七章：三元运算符（⭐）

7.1 概述

7.2 应用示例